题目内容
1.计算;(1)2$\sqrt{12}$+3$\sqrt{1\frac{1}{3}}$-$\sqrt{5\frac{1}{3}}$-$\frac{2}{3}$$\sqrt{48}$
(2)$\sqrt{48}$-$\sqrt{54}$÷2+(3-$\sqrt{3}$)(1+$\frac{1}{\sqrt{3}}$)
(3)(2$\sqrt{3}$-$\sqrt{2}$)2+$\sqrt{8}$÷$\sqrt{\frac{1}{3}}$-(3$\sqrt{3}$+2$\sqrt{5}$)(3$\sqrt{3}$-2$\sqrt{5}$).
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先变形得到原式=4$\sqrt{3}$-$\frac{3\sqrt{6}}{2}$+$\sqrt{3}$($\sqrt{3}$-1)•$\frac{1}{\sqrt{3}}$($\sqrt{3}$+1),然后利用平方差公式计算;
(3)利用二次根式的乘除法则和平方差公式计算.
解答 解:(1)原式=4$\sqrt{3}$+2$\sqrt{3}$-$\frac{4\sqrt{3}}{3}$-$\frac{8\sqrt{3}}{3}$
=2$\sqrt{3}$;
(2)原式=4$\sqrt{3}$-$\frac{3\sqrt{6}}{2}$+$\sqrt{3}$($\sqrt{3}$-1)•$\frac{1}{\sqrt{3}}$($\sqrt{3}$+1)
=4$\sqrt{3}$-$\frac{3\sqrt{6}}{2}$+2;
(3)原式=4$\sqrt{3}$-2$\sqrt{2}$+2$\sqrt{2}$×$\sqrt{3}$-(27-20)
=4$\sqrt{3}$-2$\sqrt{2}$+2$\sqrt{6}$-7.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
11.a14可以写成( )
| A. | a7+a7 | B. | a7•a7 | C. | a5•a8 | D. | a8•a2 |
 如图,在△ABC中,AB=AC=10,BC=10$\sqrt{3}$.
如图,在△ABC中,AB=AC=10,BC=10$\sqrt{3}$.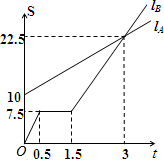 如图,LA,LB分别表示A步行与B骑车在同一路上行驶的路程S(千米)与时间t(小时)的关系.根据图象,回答下列问题:
如图,LA,LB分别表示A步行与B骑车在同一路上行驶的路程S(千米)与时间t(小时)的关系.根据图象,回答下列问题: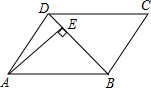 如图,在平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E.则∠DAE为20度.
如图,在平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E.则∠DAE为20度. 如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=2,则两平行线AD与BC间的距离为( )
如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=2,则两平行线AD与BC间的距离为( )