题目内容
10. 如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=2,则两平行线AD与BC间的距离为( )
如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=2,则两平行线AD与BC间的距离为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 过点P作PF⊥AD于F,作PG⊥BC于G,根据角平分线上的点到角的两边距离相等可得PF=PE,PG=PE,再根据平行线之间的距离的定义判断出EG的长即为AD、BC间的距离.
解答 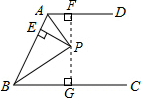 解:如图,过点P作PF⊥AD于F,作PG⊥BC于G,
解:如图,过点P作PF⊥AD于F,作PG⊥BC于G,
∵AP是∠BAD的平分线,PE⊥AB,
∴PF=PE,
同理可得PG=PE,
∵AD∥BC,
∴点F、P、G三点共线,
∴EG的长即为AD、BC间的距离,
∴平行线AD与BC间的距离为2+2=4.
故选C.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,平行线间的距离的定义,熟记性质并作辅助线构造出AD、BC间的距离的线段是解题的关键.

练习册系列答案
相关题目
5.已知△ABC中,∠A=90°,角平分线BE,CF交于点O,则∠BOC等于( )
| A. | 135° | B. | 90° | C. | 45° | D. | 145° |
15.在一次有24 000名学生参加的数学质量抽测的成绩中,随机抽取2 000名考生的数学成绩进行分析,则在该抽样中,样本指的是( )
| A. | 所抽取的2 000名考生的数学成绩 | B. | 24 000名考生的数学成绩 | ||
| C. | 2 000 | D. | 2 000名考生 |
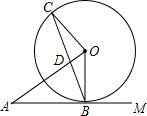 如图,⊙O与射线AM相切于点B,⊙O的半径为3.连结DA,作OC⊥OA 交⊙O于点C,连结BC,交DA于点D.
如图,⊙O与射线AM相切于点B,⊙O的半径为3.连结DA,作OC⊥OA 交⊙O于点C,连结BC,交DA于点D.