题目内容
5.(1)设a∈R,求证:抛物线y=x2+(a+2)x-2a+1都经过一个定点,且顶点都落在一条抛物线上.(2)若关于x的方程x2+(a+2)x-2a+1=0有两个不等实根,求其较大根的取值范围.
分析 (1)令f(x)=x2+(a+2)x-2a+1,将其进行转化为x2+2x+1+a(x-2),由于该函数经过定点,则与a值无关,所以x=2,将其代入抛物线解析式求得相应的y值即可得到该定点坐标,利用抛物线顶点坐标公式得到y与x的函数关系;
(2)利用求根公式求得该方程的较大根,结合二次根式的性质和根的判别式来求其取值范围.
解答 解:(1)令f(x)=x2+(a+2)x-2a+1=x2+2x+1+a(x-2),
∵抛物线y=x2+(a+2)x-2a+1都经过一个定点,
∴x-2=0即x=2,
把x=2代入得到:y=22+2×2+1=9,
即该抛物线过定点 (2,9),该抛物线的顶点坐标为x=-$\frac{a+2}{2}$,y=$\frac{4(1-2a)-(a+2)^{2}}{4}$=-$\frac{{a}^{2}+12a}{4}$
消去a,得y=-x2+4x+5,
即顶点都落在一条抛物线y=-x2+4x+5上.
(2)关于x的方程x2+(a+2)x-2a+1=0的大根为:
x=$\frac{-(a+2)+\sqrt{(a+2)^{2}-4(1-2a)}}{2}$,
=$\frac{-(a+2)+\sqrt{{a}^{2}+12}}{2}$,
=$\frac{-(a+2)+\sqrt{(a+6)^{2}-36}}{2}$.
令a+6=2k,则
x=$\frac{-(2k-4)+\sqrt{4{k}^{2}-36}}{2}$=$\sqrt{{k}^{2}-9}$-k+2.
由判别式△=(a+2)2-4(-2a+1)>0得:k>3或k<-3.
当k<-3时,x>5;
当k>3时,x=2-$\frac{9}{\sqrt{{k}^{2}-9}+k}$,可得-1<x<2.
综上可得,方程的大根x的取值范围为(-1,2)∪(5,+∞).
点评 本题主要考查了一元二次方程根的分布问题的解法,方程的根与函数零点间的关系,二次函数的图象和性质,转化化归数形结合的思想方法.

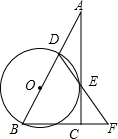 如图,在Rt△ABC中,△ACB=90°,D是AB边上的一点,以BD为直径的⊙O与AC相切于点E,连接DE并延长,与BC的延长线交于点F.
如图,在Rt△ABC中,△ACB=90°,D是AB边上的一点,以BD为直径的⊙O与AC相切于点E,连接DE并延长,与BC的延长线交于点F.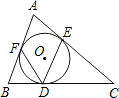 如图,△ABC的内切圆为⊙O,切点分别为D、E、F,若∠A=58°,求∠EDF的度数.
如图,△ABC的内切圆为⊙O,切点分别为D、E、F,若∠A=58°,求∠EDF的度数.
 不同的中文代表不同的数字,则“中国福州”这个四位数是1098.
不同的中文代表不同的数字,则“中国福州”这个四位数是1098.