题目内容
12．
如图，直线AB，CD相交于O，OM为∠AOD的平分线，∠1：∠2=2：3，求∠3的度数．
分析 根据OM为∠AOD的平分线，所以∠2=∠MOD，由∠1：∠2=2：3，所以设∠1=2x，∠2=3x，则∠MOD=3x，根据平角得：∠1+∠2+∠MOD=2x+3x+3x=180°，求出x，再根据根据对顶角相等，∠AOD=∠3，即可解答．
解答 解：∵OM为∠AOD的平分线，
∴∠2=∠MOD，
∵∠1：∠2=2：3，
∴设∠1=2x，∠2=3x，则∠MOD=3x，
根据平角得：∠1+∠2+∠MOD=2x+3x+3x=180°，
解得：x=22.5°，
∴∠2=∠MOD=67.5°，
∴∠AOD=∠2+∠MOD=135°，
根据对顶角相等，
∴∠AOD=∠3=135°．
点评 本题考查对顶角、邻补角，解决本题的关键是设出∠1，∠2，列出方程．
练习册系列答案
相关题目
2．中原宏发家具厂计划用甲种板材210m2，乙种板材250m2生产A、B两种款式的家具共50套，A、B两种款式的家具每套所需板材及获利情况如下表：
设生产A款家具x套，用这些板材生产的A、B两种款式的家具所获利润为y元．
（1）求y与x之间的函数关系式，并求出自变量x的取值范围；
（2）用这些板材生产A、B两种款式的家具时，如何安排可获利最大？
| 甲种板材（m2/套） | 乙种板材（m2/套） | 获利（元/套） | |
| A款 | 3 | 7 | 600 |
| B款 | 5 | 3 | 400 |
（1）求y与x之间的函数关系式，并求出自变量x的取值范围；
（2）用这些板材生产A、B两种款式的家具时，如何安排可获利最大？
在△ABC中，∠ABC=∠C=2∠A，BD是∠ABC的角平分线，求∠A与∠ADB的度数．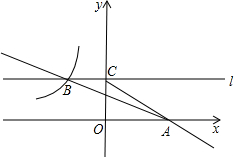
如图，在平面直角坐标系xOy中，直线y=-$\frac{1}{3}$+b与x轴交于点A，与双曲线y=-$\frac{6}{x}$在第二象限内交于点B（-3，a）．