题目内容
17.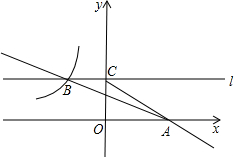 如图,在平面直角坐标系xOy中,直线y=-$\frac{1}{3}$+b与x轴交于点A,与双曲线y=-$\frac{6}{x}$在第二象限内交于点B(-3,a).
如图,在平面直角坐标系xOy中,直线y=-$\frac{1}{3}$+b与x轴交于点A,与双曲线y=-$\frac{6}{x}$在第二象限内交于点B(-3,a).(1)求a和b的值;
(2)过点B作直线l平行x轴交y轴于点C,若点P是x轴上的一点,当△BPC周长最小时,求点P的坐标;
(3)若点D在第二象限双曲线上运动,满足S△ABD=S△ABO,求点D的坐标.
分析 (1)先把B(-3,a)代入反比例函数解析式可计算出a=2,得到B点坐标,然后把B点坐标代入y=-$\frac{1}{3}$x+b可计算出b的值;
(2)作C关于x轴的对称点C′,连接BC′交x轴于P,此时,△BPC周长最小,先求得C的对称点的坐标,然后利用待定系数法求得直线BC′的解析式为y=-$\frac{4}{3}$x-2,令y=0,则求得P的坐标;
(3)设D(x,-$\frac{6}{x}$),作DE⊥x轴于E,BF⊥x轴于F,先求得S△AOB=3,然后根据S△ABD=S△ABF+S梯形BDEF-S△ADE=3,列出关于x的方程,解方程即可求得D的坐标.
解答 解:(1)把B(-3,a)代入y=-$\frac{6}{x}$得-3a=-6,解得a=2,
则B点坐标为(-3,2)
把B(-3,2)代入y=-$\frac{1}{3}$x+b得1+b=2,解得b=1;
(2)如图1,作C关于x轴的对称点C′,连接BC′交x轴于P,此时,△BPC周长最小,
∵B(-3,2),
∴C(0,2),
∴C′(0,-2),
设直线BC′的解析式为y=mx+n,
∴$\left\{\begin{array}{l}{-3m+m=2}\\{n=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-\frac{4}{3}}\\{n=-2}\end{array}\right.$,
∴直线BC′的解析式为y=-$\frac{4}{3}$x-2,
令y=0,则求得x=-$\frac{3}{2}$,
∴P(-$\frac{3}{2}$,0);
(3)如图2,设D(x,-$\frac{6}{x}$),作DE⊥x轴于E,BF⊥x轴于F,
∵由直线y=-$\frac{1}{3}$x+1可知A(3,0),
∴S△AOB=$\frac{1}{2}$×3×2=3,
∴S△ABD=S△ABF+S梯形BDEF-S△ADE=3或S△ABD=S梯形BDEF+S△ADE-S△ABF=3,
即$\frac{1}{2}$×6×2+$\frac{1}{2}$(-x-3)(-$\frac{6}{x}$+2)-$\frac{1}{2}$(3-x)(-$\frac{6}{x}$)=3或$\frac{1}{2}$(3+x)(-$\frac{6}{x}$+2)+$\frac{1}{2}$(3-x)(-$\frac{6}{x}$)-$\frac{1}{2}$×6×2=3,
整理得,x2=18或x2-6x-18=0
∵x<0,
∴x=-3$\sqrt{2}$或x=3-3$\sqrt{3}$
∴D(-3$\sqrt{2}$,$\sqrt{2}$)或(3-3$\sqrt{3}$,1+$\sqrt{3}$).
点评 本题考查了反比例函数和一次函数的交点问题,轴对称-最短路线问题,三角形的面积等,反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式.

 名校课堂系列答案
名校课堂系列答案| A. | x<1 | B. | -1<x<1 | C. | x>-1 | D. | x<-1或x>1 |
| A. | x=2是不等式3x>5的一个解 | B. | x=2是不等式3x>5的解 | ||
| C. | x=2是不等式3x>5的唯一解 | D. | x=2不是不等式3x>5的解 |
 如图:将一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,ED′的延长线与BC交于点G.若∠BFC′=70°,则∠1=( )
如图:将一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,ED′的延长线与BC交于点G.若∠BFC′=70°,则∠1=( )| A. | 100° | B. | 110° | C. | 120° | D. | 125° |
 如图所示,已知ABC,∠C=90°,AC=BC=4,现将△ABC沿CB方向平移到△A1B1C1的位置.
如图所示,已知ABC,∠C=90°,AC=BC=4,现将△ABC沿CB方向平移到△A1B1C1的位置. 如图,直线AB,CD相交于O,OM为∠AOD的平分线,∠1:∠2=2:3,求∠3的度数.
如图,直线AB,CD相交于O,OM为∠AOD的平分线,∠1:∠2=2:3,求∠3的度数. 如图,在△ABC中,∠C=90°,AE,BE是△ABC的两个内角的平分线,AF,BF是△ABC的两个外角的平分线.求∠E,∠F的度数.
如图,在△ABC中,∠C=90°,AE,BE是△ABC的两个内角的平分线,AF,BF是△ABC的两个外角的平分线.求∠E,∠F的度数.