题目内容
一个圆作滚动运动(如图),它从位置A开始,在与它相同的其它六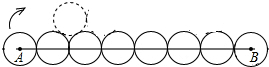 个圆上部滚动,到达B位置(六个圆的圆心与A、B在同一直线上),则该圆上某一定点绕其圆心共滚过的圈数为( )圈.
个圆上部滚动,到达B位置(六个圆的圆心与A、B在同一直线上),则该圆上某一定点绕其圆心共滚过的圈数为( )圈.
 个圆上部滚动,到达B位置(六个圆的圆心与A、B在同一直线上),则该圆上某一定点绕其圆心共滚过的圈数为( )圈.
个圆上部滚动,到达B位置(六个圆的圆心与A、B在同一直线上),则该圆上某一定点绕其圆心共滚过的圈数为( )圈.| A、3 | ||
B、
| ||
C、
| ||
D、
|
考点:弧长的计算
专题:
分析:它从A位置开始,滚过与它相同的其他六个圆的上部,到达B位置.则该圆共滚过了6段弧长,其中有2段是半径为2r,圆心角为120度,4段是半径为2r,圆心角为60度的弧长,所以可求得.
解答:解:弧长=
=
πr,
小圆的周长=2πr,
所以该圆共滚过了
πr÷2πr=
πr.
故选B.
| 120π×2r×2+60π×2r×4 |
| 180 |
| 16 |
| 3 |
小圆的周长=2πr,
所以该圆共滚过了
| 16 |
| 3 |
| 8 |
| 3 |
故选B.
点评:考查了弧长的计算.关键是理解该点所经过的路线三个扇形的弧长.

练习册系列答案
相关题目
 如图(1),把一个长为m,宽为n的矩形(m>n)沿虚线剪开拼接成图(2),成为在一角去掉一个小正方形后的大正方形,则这个去掉的小正方形的边长为( )
如图(1),把一个长为m,宽为n的矩形(m>n)沿虚线剪开拼接成图(2),成为在一角去掉一个小正方形后的大正方形,则这个去掉的小正方形的边长为( )A、
| ||
| B、m-n | ||
C、
| ||
D、
|
边长为整数,周长为20的等腰三角形个数是( )
| A、2个 | B、3个 | C、4个 | D、5个 |
已知a为实数,且a3+a2-a+2=0,则(a+1)8+(a+1)9+(a+1)10的值是( )
| A、-3 | B、3 | C、-1 | D、1 |
 菱形,要求菱形的顶点均在格点上.
菱形,要求菱形的顶点均在格点上.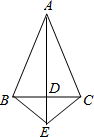 (1)如图,AB=AC,AE⊥BC于点D,求证:BE=CE.
(1)如图,AB=AC,AE⊥BC于点D,求证:BE=CE. 如图,在锐角△ABC中,CD,BE分别是AB,AC上的高,且CD,BE交于点P,若∠A=80°,∠BPC的度数是
如图,在锐角△ABC中,CD,BE分别是AB,AC上的高,且CD,BE交于点P,若∠A=80°,∠BPC的度数是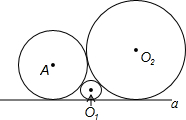 如图,已知⊙A,⊙O1,⊙O2两两相切,且都与直线a相切,若⊙A的半径为1,⊙O1与⊙O2的半径分别为x,y(y≥1).则y与x的函数关系式为
如图,已知⊙A,⊙O1,⊙O2两两相切,且都与直线a相切,若⊙A的半径为1,⊙O1与⊙O2的半径分别为x,y(y≥1).则y与x的函数关系式为