题目内容
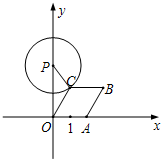 如图,已知点A从(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O,A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,当点A在运动过程中,⊙P与菱形OABC的边所在直线相切时,t=
如图,已知点A从(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O,A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,当点A在运动过程中,⊙P与菱形OABC的边所在直线相切时,t=考点:切线的性质,坐标与图形性质,菱形的性质
专题:计算题,压轴题
分析:⊙P与菱形OABC的边所在直线相切,则可与OC相切;或与OA相切;或与AB相切,应分三种情况探讨:①当圆P与OC相切时,如图1所示,由切线的性质得到PC垂直于OC,再由OA=+t,根据菱形的边长相等得到OC=1+t,由∠AOC的度数求出∠POC为30°,在直角三角形POC中,利用锐角三角函数定义表示出cos30°=
,表示出OC,等于1+t列出关于t的方程,求出方程的解即可得到t的值;②当圆P与OA,即与x轴相切时,过P作PE垂直于OC,又PC=PO,利用三线合一得到E为OC的中点,OE为OC的一半,而OE=OPcos30°,列出关于t的方程,求出方程的解即可得到t的值;③当圆P与AB所在的直线相切时,设切点为F,PF与OC交于点G,由切线的性质得到PF垂直于AB,则PF垂直于OC,由CD=FG,在直角三角形OCD中,利用锐角三角函数定义由OC表示出CD,即为FG,在直角三角形OPG中,利用OP表示出PG,用PG+GF表示出PF,根据PF=PC,表示出PC,过C作CH垂直于y轴,在直角三角形PHC中,利用勾股定理列出关于t的方程,求出方程的解即可得到t的值,综上,得到所有满足题意的t的值.
| OC |
| OP |
解答:解:分三种情况考虑:
①当⊙P与OC相切时(如图1),切点为C,此时PC⊥OC,
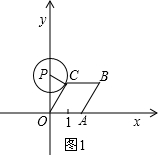 ∵OA=1+t,四边形OABC为菱形,
∵OA=1+t,四边形OABC为菱形,
∴OC=1+t,
∴OC=OPcos30°,
∴1+t=3•
,
∴t=
-1;
②当⊙P与OA,即与x轴相切时(如图2),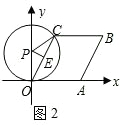 切点为O,PC=OP=3,
切点为O,PC=OP=3,
过P作PE⊥OC于E,则OE=
OC,
∴
=OPcos30°=
,
∴t=3
-1;
③当⊙P与AB所在直线相切时(如图3),
设切点为F,PF交OC于G,则PF⊥OC,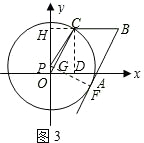
∴FG=CD=(1+t)sin60°=
(1+t),
∴PC=PF=OPsin30°+
(1+t)=
+
(1+t),
过C作CH⊥y轴于H,
在Rt△PHC中,利用勾股定理得:PH2+CH2=PC2,
∴(
)2+(
-3)2=(
+
)2,
化简得:(t+1)2-18
(t+1)+27=0,
解得:t+1=9
±6
,
∵t=9
-6
-1<0,
∴t=9
+6
-1,
∴所求t的值为
-1或3
-1或9
+6
-1.
故答案为:
-1或3
-1或9
+6
-1.
①当⊙P与OC相切时(如图1),切点为C,此时PC⊥OC,
 ∵OA=1+t,四边形OABC为菱形,
∵OA=1+t,四边形OABC为菱形,∴OC=1+t,
∴OC=OPcos30°,
∴1+t=3•
| ||
| 2 |
∴t=
3
| ||
| 2 |
②当⊙P与OA,即与x轴相切时(如图2),
 切点为O,PC=OP=3,
切点为O,PC=OP=3,过P作PE⊥OC于E,则OE=
| 1 |
| 2 |
∴
| 1+t |
| 2 |
3
| ||
| 2 |
∴t=3
| 3 |
③当⊙P与AB所在直线相切时(如图3),
设切点为F,PF交OC于G,则PF⊥OC,

∴FG=CD=(1+t)sin60°=
| ||
| 2 |
∴PC=PF=OPsin30°+
| ||
| 2 |
| 3 |
| 2 |
| ||
| 2 |
过C作CH⊥y轴于H,
在Rt△PHC中,利用勾股定理得:PH2+CH2=PC2,
∴(
| 1+t |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| ||
| 2 |
化简得:(t+1)2-18
| 3 |
解得:t+1=9
| 3 |
| 6 |
∵t=9
| 3 |
| 6 |
∴t=9
| 3 |
| 6 |
∴所求t的值为
3
| ||
| 2 |
| 3 |
| 3 |
| 6 |
故答案为:
3
| ||
| 2 |
| 3 |
| 3 |
| 6 |
点评:此题考查了切线的性质,菱形的性质,特殊角的三角函数值,及勾股定理的运用,利用了分类讨论的思想,熟练掌握切线的性质是解本题的关键,同时注意锐角三角函数定义及特殊角的三角函数值的运用.

练习册系列答案
相关题目
边长为整数,周长为20的等腰三角形个数是( )
| A、2个 | B、3个 | C、4个 | D、5个 |
一辆标致307以30m/s的速度在汉宜高速公路上疾驰,司机突然发现前方路面有情况,紧急刹车后小车滑行了75m后停止,给出如下判断:①从刹车到停车用了5秒;②从刹车到停车平均每秒车速减少值为6m/s;③刹车后汽车滑行到48m时约用了2s钟.
其中判断正确的是( )
其中判断正确的是( )
| A、①② | B、②③ | C、①③ | D、①②③ |
两圆的直径分别为4和6,圆心距为10,则两圆的位置关系为( )
| A、外离 | B、外切 | C、相交 | D、内切 |
 如图,在锐角△ABC中,CD,BE分别是AB,AC上的高,且CD,BE交于点P,若∠A=80°,∠BPC的度数是
如图,在锐角△ABC中,CD,BE分别是AB,AC上的高,且CD,BE交于点P,若∠A=80°,∠BPC的度数是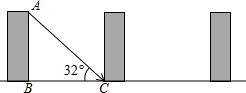 为32°,在公寓的采光不受影响(冬季正午最底层受到阳光照射)的情况下,公寓的高为AB,相邻两公寓间的最小距离为BC.
为32°,在公寓的采光不受影响(冬季正午最底层受到阳光照射)的情况下,公寓的高为AB,相邻两公寓间的最小距离为BC.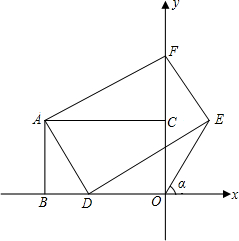 的一个动点,连接AD,过A作AD的垂线交y轴于F点,并以AF、AD为边作矩形ADEF.
的一个动点,连接AD,过A作AD的垂线交y轴于F点,并以AF、AD为边作矩形ADEF.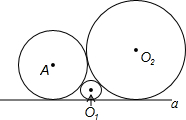 如图,已知⊙A,⊙O1,⊙O2两两相切,且都与直线a相切,若⊙A的半径为1,⊙O1与⊙O2的半径分别为x,y(y≥1).则y与x的函数关系式为
如图,已知⊙A,⊙O1,⊙O2两两相切,且都与直线a相切,若⊙A的半径为1,⊙O1与⊙O2的半径分别为x,y(y≥1).则y与x的函数关系式为