题目内容
 已知⊙O直径为2,△ABC为⊙O内接三角形,点I为△ABC内心,求ID长为
已知⊙O直径为2,△ABC为⊙O内接三角形,点I为△ABC内心,求ID长为考点:三角形的内切圆与内心
专题:计算题
分析:连结BD,BI,BD,CD,如图,根据三角形内心的性质得∠2=∠4,∠5=∠6,再根据圆周角定理得∠7=∠4,则∠2=∠7,接着利用三角形外角性质得∠1=∠2+∠5,于是得到∠1=∠7+∠6,即∠1=∠DBI,所以ID=BD,再证明△BDC为等腰直角三角形,然后根据等腰直角三角形的性质得BD=
BC=
,即有ID=
.
| ||
| 2 |
| 2 |
| 2 |
解答:解:连结BD,BI,BD,CD,如图,
∵点I为△ABC内心,
∴AD平分∠BAC,BI平分∠ABC,
∴∠2=∠4,∠5=∠6,
∵∠7=∠4,
∴∠2=∠7,
∵∠1=∠2+∠5,
∴∠1=∠7+∠6,即∠1=∠DBI,
∴ID=BD,
∵BC为直径,
∴∠BDC=90°,
∵∠2=∠4,
∴
=
,
∴BD=CD,
∴△BDC为等腰直角三角形,
∴BD=
BC=
×2=
,
∴ID=
.
故答案为
.

∵点I为△ABC内心,
∴AD平分∠BAC,BI平分∠ABC,
∴∠2=∠4,∠5=∠6,
∵∠7=∠4,
∴∠2=∠7,
∵∠1=∠2+∠5,
∴∠1=∠7+∠6,即∠1=∠DBI,
∴ID=BD,
∵BC为直径,
∴∠BDC=90°,
∵∠2=∠4,
∴
 |
| BD |
 |
| CD |
∴BD=CD,
∴△BDC为等腰直角三角形,
∴BD=
| ||
| 2 |
| ||
| 2 |
| 2 |
∴ID=
| 2 |
故答案为
| 2 |
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了圆周角定理.

练习册系列答案
相关题目
全面贯彻落实“大气十条”,抓好大气污染防治,是今年环保工作的重中之重.其中推进燃煤电厂脱硫改造15000 000千瓦是《政府工作报告》中确定的重点任务之一.将数据15 000 000用科学记数法表示为( )
| A、15×106 |
| B、1.5×107 |
| C、1.5×108 |
| D、0.15×108 |
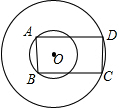 如图,两同心圆的半径分别为6、10,矩形ABCD的边AB、CD分别为两圆的弦.当矩形面积取最大值时,其周长为
如图,两同心圆的半径分别为6、10,矩形ABCD的边AB、CD分别为两圆的弦.当矩形面积取最大值时,其周长为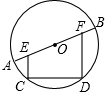 如图,AB是直径,CD是弦,过点C和D作EC⊥CD、FD⊥CD,分别交AB于点E、F.试猜想:AE与BF是何关系.说明理由.
如图,AB是直径,CD是弦,过点C和D作EC⊥CD、FD⊥CD,分别交AB于点E、F.试猜想:AE与BF是何关系.说明理由. 如图,DE∥AB,AD∥BC,求证:△EAD∽△ACB.
如图,DE∥AB,AD∥BC,求证:△EAD∽△ACB.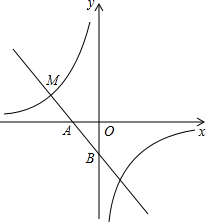 如图,一次函数y=-3x-1的图象与x轴交于点A,与y轴交于点B,与反比例函数y=
如图,一次函数y=-3x-1的图象与x轴交于点A,与y轴交于点B,与反比例函数y=