题目内容
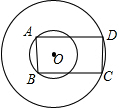 如图,两同心圆的半径分别为6、10,矩形ABCD的边AB、CD分别为两圆的弦.当矩形面积取最大值时,其周长为
如图,两同心圆的半径分别为6、10,矩形ABCD的边AB、CD分别为两圆的弦.当矩形面积取最大值时,其周长为考点:垂径定理,勾股定理,矩形的性质
专题:
分析:先求出矩形ABCD的面积=4三角形AOD的面积,求出三角形AOD的面积最大时,∠AOD=90°,求出OM,即可求出AB,即可求出周长.
解答:解:连接OA,OD,作OP⊥AB于P,OM⊥AD于M,ON⊥CD于N,
过D作DE⊥OA于E,
∵矩形APND的面积是AD×OM,△AOD的面积=
AD×OM,矩形BCNP的面积是OM×BC,
∴矩形的面积是三角形AOD的面积的4倍,
在Rt△DEO中,DE=OD×sin∠DOE=OD×sin∠AOD,
∵OA,OD的长是定值,S△AOD=
×OA×OD×sin∠AOD,
∴要使矩形ABCD的面积最大,必须△AOD的面积最大,
即当∠AOD的正弦值最大时,三角形AOD的面积最大,
∵当∠AOD≤90°时,正弦值随角度的增大而增大,
即当∠AOD=90°,S△AOD最大,
则勾股定理得:AD=
=2
,
根据三角形的面积公式求得OM=
,即AB=
.则矩形ABCD的周长是2(2
+
)=
,
故答案为:
.

过D作DE⊥OA于E,
∵矩形APND的面积是AD×OM,△AOD的面积=
| 1 |
| 2 |
∴矩形的面积是三角形AOD的面积的4倍,
在Rt△DEO中,DE=OD×sin∠DOE=OD×sin∠AOD,
∵OA,OD的长是定值,S△AOD=
| 1 |
| 2 |
∴要使矩形ABCD的面积最大,必须△AOD的面积最大,
即当∠AOD的正弦值最大时,三角形AOD的面积最大,
∵当∠AOD≤90°时,正弦值随角度的增大而增大,
即当∠AOD=90°,S△AOD最大,
则勾股定理得:AD=
| 62+102 |
| 34 |
根据三角形的面积公式求得OM=
15
| ||
| 17 |
30
| ||
| 17 |
| 34 |
30
| ||
| 17 |
128
| ||
| 17 |
故答案为:
128
| ||
| 17 |
点评:本题考查了垂径定理,锐角三角函数的定义,勾股定理,矩形的性质的应用,解此题的关键是能正确作出辅助线构造直角三角形进而求出∠AOD的值,有一定的难度.

练习册系列答案
相关题目

 如图,矩形ABCD中,AB=4,AD=9,点M在BC上,且BM:MC=1:2,DE⊥AM于点E,求DE的长.
如图,矩形ABCD中,AB=4,AD=9,点M在BC上,且BM:MC=1:2,DE⊥AM于点E,求DE的长. 已知⊙O直径为2,△ABC为⊙O内接三角形,点I为△ABC内心,求ID长为
已知⊙O直径为2,△ABC为⊙O内接三角形,点I为△ABC内心,求ID长为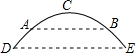 如图是某地一座抛物线形拱桥,桥拱在竖直平面内,与水面相交于A,B两点,拱桥最高点C到AB的距离为9m,AB=36m,D,E为拱桥底部的两点,且DE∥AB,点E到直线AB的距离为7m.建立平面直角坐标系,求:
如图是某地一座抛物线形拱桥,桥拱在竖直平面内,与水面相交于A,B两点,拱桥最高点C到AB的距离为9m,AB=36m,D,E为拱桥底部的两点,且DE∥AB,点E到直线AB的距离为7m.建立平面直角坐标系,求: