题目内容
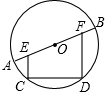如图，AB是直径，CD是弦，过点C和D作EC⊥CD、FD⊥CD，分别交AB于点E、F．试猜想：AE与BF是何关系．说明理由．考点：垂径定理,梯形中位线定理
专题：
分析：作OM⊥EF于M点，根据垂径定理得CM=DM，再证明OM为梯形CDFE的中位线，则OE=OF，易得AE=BF．
解答：解：AE=BF．
理由：作OM⊥EF于M点，则CM=DM，
∵EC⊥CD，FD⊥CD，
∴CE∥OM∥DF，
∴OM为梯形CDFE的中位线，
∴OE=OF，
∴OA-OE=OB-OF，即AE=BF．
理由：作OM⊥EF于M点，则CM=DM，∵EC⊥CD，FD⊥CD，
∴CE∥OM∥DF，
∴OM为梯形CDFE的中位线，
∴OE=OF，
∴OA-OE=OB-OF，即AE=BF．
点评：本题考查的是垂径定理，根据题意作出辅助线，构造出梯形的中位线是解答此题的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
已知△ABC，△ADE均为等腰直角三角形，且∠BAC=∠DAE=90°，BD的延长线交AC于点F，交CE于G．
已知⊙O直径为2，△ABC为⊙O内接三角形，点I为△ABC内心，求ID长为
如图，时钟的时针、分针、秒针均是匀速转动的，它们分别用OB、OA、OC表示．
如图，每个小正方形的边长均为a，则阴影部分的面积为（ ）| A、5a2 | ||
| B、4a2 | ||
| C、3a2 | ||
D、
|
