题目内容
13. 请从以下两小题中任选一个作答,若多选,则按所选的第一题计分
请从以下两小题中任选一个作答,若多选,则按所选的第一题计分A.边长2cm的正六边形的边心距是$\sqrt{3}$cm
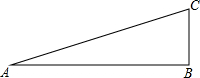
B.小明同学在距某电视塔塔底水平距离500米处,看塔顶的仰角为20°,(不考虑身高因素),则此塔高约为182米(用科学计算器计算,结果保留整数)
分析 A.过点O作OM⊥AB与M,连接OB,先求出BM,再根据tan∠BOM=$\frac{BM}{OM}$,得出OM=$\frac{BM}{tan∠BOM}$,最后代入计算即可;
B.根据tan∠CAB=$\frac{BC}{AB}$,BC=tan∠CAB×AB,再代入计算即可.
解答 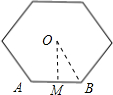 解:A.如图:过点O作OM⊥AB与M,连接OB,
解:A.如图:过点O作OM⊥AB与M,连接OB,
∵AB=2cm,
∴BM=$\frac{1}{2}$AB=1cm,
∵tan∠BOM=$\frac{BM}{OM}$,∠BOM=30°,
∴OM=$\frac{BM}{tan∠BOM}$=$\frac{1}{tan30°}$=$\sqrt{3}$(cm),
故答案为:$\sqrt{3}$;
B.∵tan∠CAB=$\frac{BC}{AB}$,AB=500,∠CAB=20°,
∴BC=tan20°×500≈0.3640×500=182;
故答案为;182.
点评 本题考查了解直角三角形,用到的知识点是仰角的定义、正六边形的性质、特殊角的三角函数值等,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
1.直线y=kx(k>0)与双曲线y=$\frac{2}{x}$交于A,B两点,若A,B两点的坐标分别为A(x1,y1),B(x2,y2),则(x1-x2)(y1-y2)的值为( )
| A. | -4 | B. | 0 | C. | 4 | D. | 8 |
8. 如图,直线a∥b,直线a⊥c,若∠1=70°,则∠2=( )
如图,直线a∥b,直线a⊥c,若∠1=70°,则∠2=( )
 如图,直线a∥b,直线a⊥c,若∠1=70°,则∠2=( )
如图,直线a∥b,直线a⊥c,若∠1=70°,则∠2=( )| A. | 70° | B. | 90° | C. | 20° | D. | 80° |
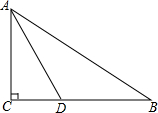 如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于点D.
如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于点D.