题目内容
2.已知y关于x的函数y=(m+$\frac{1}{2}$)(n-1)x|n|+m2-$\frac{1}{4}$是正比例函数.(1)求m,n的值;
(2)画出它的图象;
(3)写出它的一条性质.
分析 (1)根据正比例函数的定义进行解答;
(2)根据两点法画出函数图象;
(3)根据正比例函数的性质写出即可.
解答 解:(1)∵y关于x的函数y=(m+$\frac{1}{2}$)(n-1)x|n|+m2-$\frac{1}{4}$是正比例函数,
∴${m}^{2}-\frac{1}{4}=0$,|n|=1,
解得:m=±$\frac{1}{2}$,n=±1,
∵$(m+\frac{1}{2})(n-1)≠0$,
∴m$≠-\frac{1}{2}$,n≠1,
∴m=$\frac{1}{2}$,n=-1.
(2)函数解析式为:y=-2x,如图,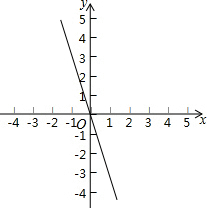
(3)y=-2x的图象过第二、四象限,y随x的增大而减小.
点评 本题考查了正比例函数的定义,性质,解决本题的关键是熟记正比例函数的定义和性质.

练习册系列答案
相关题目
12.一元二次方程(1-k)x2-2x-1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k<2且k≠1 | B. | k>2且k≠1 | C. | k>2 | D. | k<2 |
 请从以下两小题中任选一个作答,若多选,则按所选的第一题计分
请从以下两小题中任选一个作答,若多选,则按所选的第一题计分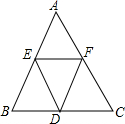 如图所示,AB=BC=CA=2,将△ABC的三边均分为二等分,并按图中那样构成,则图中有几个三角形?请用你手中的刻度尺度量一下,它们分别是什么形状的三角形?
如图所示,AB=BC=CA=2,将△ABC的三边均分为二等分,并按图中那样构成,则图中有几个三角形?请用你手中的刻度尺度量一下,它们分别是什么形状的三角形?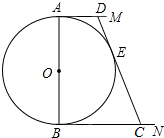 如图,⊙O的直径AB=12,AM,BN是⊙O的两条切线,DC切⊙O于E,交BN于C,设AD=x,BC=y.
如图,⊙O的直径AB=12,AM,BN是⊙O的两条切线,DC切⊙O于E,交BN于C,设AD=x,BC=y.