题目内容
3.(1)不画图象仅从函数解析式,判断直线y=3x与y=3x-1的位置关系是平行,直线y=3x向下平移4个单位就可以得到y=3x-4;(2)不画图象仅从函数解析式,判断直线y=$\frac{3}{5}$x-4与y=$\frac{3}{5}$x+4的位置关系是平行,直线y=$\frac{3}{5}$x-4向上平移8个单位就可以得到y=$\frac{3}{5}$x+4.
分析 (1)根据两条直线的k值相同都是3,而b值不相同可知直线y=3x与y=3x-1平行,根据“上加下减”的平移规律可得直线y=3x向下平移4个单位就可以得到y=3x-4;
(2)根据两条直线的k值相同都是$\frac{3}{5}$,而b值不相同可知直线y=$\frac{3}{5}$x-4与y=$\frac{3}{5}$x+4平行,根据“上加下减”的平移规律可得直线y=$\frac{3}{5}$x-4向上平移8个单位就可以得到y=$\frac{3}{5}$x+4.
解答 解:(1)∵两条直线的k值相同都是3,而b值不相同,
∴直线y=3x与y=3x-1平行,
根据“上加下减”的平移规律可得直线y=3x向下平移4个单位就可以得到y=3x-4;
(2)∵两条直线的k值相同都是$\frac{3}{5}$,而b值不相同,
∴直线y=$\frac{3}{5}$x-4与y=$\frac{3}{5}$x+4平行,
根据“上加下减”的平移规律可得直线y=$\frac{3}{5}$x-4向上平移8个单位就可以得到y=$\frac{3}{5}$x+4.
故答案为平行,下,4;平行,上,8.
点评 本题考查了一次函数图象与几何变换,掌握“左加右减,上加下减”的平移规律是解题的关键,也考查了两条直线的位置关系.

练习册系列答案
相关题目
3.把一张纸剪成5块,从所得纸片中取一块,把此块再剪成5块,然后从这5块中取出一块,把此块又剪成5块,这样类似进行n次后(n是正整数),共得纸片的总块数是( )
| A. | 5n+4 | B. | 5n+5 | C. | 4n+1 | D. | 4n+4 |
8. 如图所示为一个无盖长方体盒子的展开图(重叠部分不计),根据图中数据,可知该无盖长方体的容积为( )
如图所示为一个无盖长方体盒子的展开图(重叠部分不计),根据图中数据,可知该无盖长方体的容积为( )
 如图所示为一个无盖长方体盒子的展开图(重叠部分不计),根据图中数据,可知该无盖长方体的容积为( )
如图所示为一个无盖长方体盒子的展开图(重叠部分不计),根据图中数据,可知该无盖长方体的容积为( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
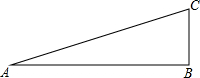 请从以下两小题中任选一个作答,若多选,则按所选的第一题计分
请从以下两小题中任选一个作答,若多选,则按所选的第一题计分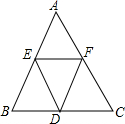 如图所示,AB=BC=CA=2,将△ABC的三边均分为二等分,并按图中那样构成,则图中有几个三角形?请用你手中的刻度尺度量一下,它们分别是什么形状的三角形?
如图所示,AB=BC=CA=2,将△ABC的三边均分为二等分,并按图中那样构成,则图中有几个三角形?请用你手中的刻度尺度量一下,它们分别是什么形状的三角形?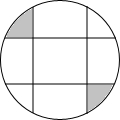 如图,圆中有四条弦,每一条弦都将圆分割成面积比为1:3的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为π.
如图,圆中有四条弦,每一条弦都将圆分割成面积比为1:3的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为π.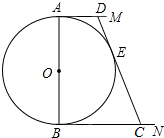 如图,⊙O的直径AB=12,AM,BN是⊙O的两条切线,DC切⊙O于E,交BN于C,设AD=x,BC=y.
如图,⊙O的直径AB=12,AM,BN是⊙O的两条切线,DC切⊙O于E,交BN于C,设AD=x,BC=y.