题目内容
16.由命题“有两边及其中一边上的高对应相等的两个锐角三角形全等”写出已知,求证,并证明.分析 根据题意首先写出已知和求证,进而利用全等三角形的判定与性质得出Rt△ADB≌Rt△A′D′B′以及∠B=∠B′进而得出△ABC≌△A′B′C′.
解答 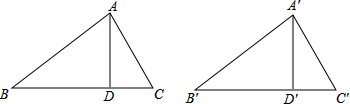 如图,△ABC与△A′B′C′,BC=B′C′,AB=A′B′,AD⊥BC,A′D′⊥B′C′,且AD=A′D′,
如图,△ABC与△A′B′C′,BC=B′C′,AB=A′B′,AD⊥BC,A′D′⊥B′C′,且AD=A′D′,
求证:△ABC≌△A′B′C′.
证明:∵AD⊥BC,A′D′⊥B′C′,
∴∠ADB=∠A′D′B′=90°,
在Rt△ADB和Rt△A′D′B′中
∵$\left\{\begin{array}{l}{AB=A′B′}\\{AD=A′D′}\end{array}\right.$,
∴Rt△ADB≌Rt△A′D′B′(HL),
∴∠B=∠B′,
在△ABC与△A′B′C′中
∵$\left\{\begin{array}{l}{AB=A′B′}\\{∠B=∠B′}\\{BC=B′C′}\end{array}\right.$,
∴△ABC≌△A′B′C′(SAS).
点评 本题考查了全等三角形判定的应用,熟练应用全等三角形的判定方法是解题关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
4.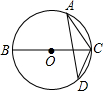 如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠ACB的度数是( )
如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠ACB的度数是( )
 如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠ACB的度数是( )
如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠ACB的度数是( )| A. | 35° | B. | 55° | C. | 65° | D. | 70° |
 如图,已知抛物线y=x2过P(2,m),过P点的直线l与抛物线只有一个公共点,求直线l的解析式.
如图,已知抛物线y=x2过P(2,m),过P点的直线l与抛物线只有一个公共点,求直线l的解析式. 已知:如图,∠1和线段m.
已知:如图,∠1和线段m. 如图,在Rt△ABC和Rt△BAD中,∠C=∠D=90°,AD平分∠CAB,BC平分∠ABD,AD、BC相交于点O,求证:OC=OD.
如图,在Rt△ABC和Rt△BAD中,∠C=∠D=90°,AD平分∠CAB,BC平分∠ABD,AD、BC相交于点O,求证:OC=OD.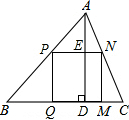 △ABC是一块钝角三角形的余料,如图所示,BC=48cm,高AD=16cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,求这个正方形零件的边长是多少?
△ABC是一块钝角三角形的余料,如图所示,BC=48cm,高AD=16cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,求这个正方形零件的边长是多少? 如图:在△ABC中,AE⊥BC,在△BDC中,DF⊥BC,AE=DF,AB=CD.求证:AC=BD.
如图:在△ABC中,AE⊥BC,在△BDC中,DF⊥BC,AE=DF,AB=CD.求证:AC=BD. 已知:如图,正方形ABCD和正三角形ADE,求证:△BCE是等腰三角形.
已知:如图,正方形ABCD和正三角形ADE,求证:△BCE是等腰三角形.