题目内容
1.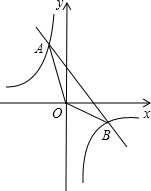 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(-1,3),B(3,a)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(-1,3),B(3,a)两点.(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式kx+b>$\frac{m}{x}$的解集;
(2)求S△AOB.
分析 (1)把A的坐标代入反比例函数解析式求得解析式,然后求得B的坐标,再用待定系数法求得一次函数的解析式;
(2)不等式kx+b>$\frac{m}{x}$的解集就是一次函数的图象在反比例函数的图象的上边时对应的x的范围;
(3)首先求得AB与y轴的交点,然后利用三角形的面积公式求解.
解答 解:(1)把A(-1,3)代入y=$\frac{m}{x}$得m=-3,
则反比例函数的解析式是y=-$\frac{3}{x}$,
当x=3时,y=-1,则B的坐标是(3,-1).
根据题意得:$\left\{\begin{array}{l}{-k+b=3}\\{3k+b=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=2}\end{array}\right.$,
则直线的解析式是y=-x+2;
(2)不等式kx+b>$\frac{m}{x}$的解集是:x<-1或0<x<3;
(3)在y=-x+2中,令x=0,则y=2,
则S△AOB=$\frac{1}{2}$×2×1+$\frac{1}{2}$×2×3=4.
点评 本题考查了反比例函数与一次函数的交点,当有两个函数的时候,着重使用一次函数,体现了方程思想,综合性较强.

练习册系列答案
相关题目
8.下列根式中,不能与$\sqrt{3}$合并的是( )
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\frac{3}{{\sqrt{3}}}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{12}$ |
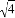 ×(2017-π)0+(
×(2017-π)0+( )-2
)-2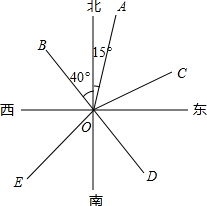 如图,OA的方向是北偏东15°,OB的方向是北偏西40°.
如图,OA的方向是北偏东15°,OB的方向是北偏西40°.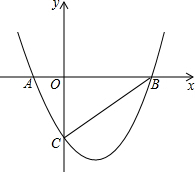 如图,抛物线y=$\frac{\sqrt{3}}{2}$x2-$\frac{\sqrt{3}}{2}$x-$\sqrt{3}$与x轴相交于点A和点B,与y轴相交于点C,连接BC,在抛物线上找点D,连接CD,若∠BCD=90°,求点D的坐标.
如图,抛物线y=$\frac{\sqrt{3}}{2}$x2-$\frac{\sqrt{3}}{2}$x-$\sqrt{3}$与x轴相交于点A和点B,与y轴相交于点C,连接BC,在抛物线上找点D,连接CD,若∠BCD=90°,求点D的坐标. 根据几何体的三视图,画出它的展开图.
根据几何体的三视图,画出它的展开图.