题目内容
4.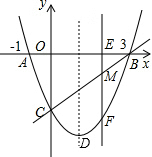 如图,抛物线与x轴交于点A(-1,0)、点B(3,0),交y轴于点C(0,-3),点M为线段BC上一动点,过点M作x轴的垂线,交x轴于点E,交抛物线于点F
如图,抛物线与x轴交于点A(-1,0)、点B(3,0),交y轴于点C(0,-3),点M为线段BC上一动点,过点M作x轴的垂线,交x轴于点E,交抛物线于点F(1)求抛物线的函数解析式;
(2)求MF的最大值及此时M点的坐标.
分析 (1)利用待定系数法即可求得二次函数的解析式;
(2)首先求得BC的解析式,则设M的横坐标是x,从而利用x表示出MF的长,利用二次函数的性质求解.
解答 解:(1)设函数的解析式是y=ax2+bx+c.
根据题意得:$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=-3}\end{array}\right.$,
则函数的解析式是y=x2-2x-3;
(2)设直线BC的解析式是y=kx+b,
则$\left\{\begin{array}{l}{3k+b=0}\\{b=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$,
则直线BC的解析式是y=x-3.
设M的横坐标是x,则M的纵坐标是x-3,F的纵坐标是x2-2x-3,
则MF=(x-3)-(x2-2x-3)=-x2+2x=-(x-1)2+1.
则当x=1是MF取得最大值是1,此时M的坐标是(1,-2).
点评 本题考查了待定系数法求函数的解析式以及二次函数的性质的应用,利用x表示出MF的长是关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
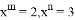 ,则
,则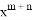 的值为___________.
的值为___________.
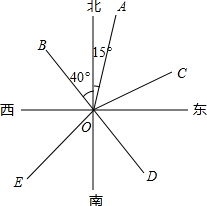 如图,OA的方向是北偏东15°,OB的方向是北偏西40°.
如图,OA的方向是北偏东15°,OB的方向是北偏西40°.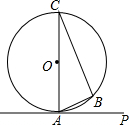 如图所示,PA是⊙O的切线,切点为A,∠PAB是切线AP与弦AB的夹角,∠C是$\widehat{AB}$所对的圆周角.
如图所示,PA是⊙O的切线,切点为A,∠PAB是切线AP与弦AB的夹角,∠C是$\widehat{AB}$所对的圆周角.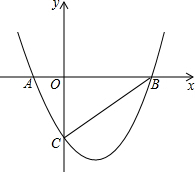 如图,抛物线y=$\frac{\sqrt{3}}{2}$x2-$\frac{\sqrt{3}}{2}$x-$\sqrt{3}$与x轴相交于点A和点B,与y轴相交于点C,连接BC,在抛物线上找点D,连接CD,若∠BCD=90°,求点D的坐标.
如图,抛物线y=$\frac{\sqrt{3}}{2}$x2-$\frac{\sqrt{3}}{2}$x-$\sqrt{3}$与x轴相交于点A和点B,与y轴相交于点C,连接BC,在抛物线上找点D,连接CD,若∠BCD=90°,求点D的坐标.