题目内容
20．
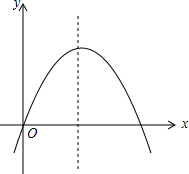已知二次函数y=ax2+bx+c的图象如图所示，记m=|a-b+c|+|2a+b+c|，n=|a+b+c|+|2a-b-c|．抛物线与x轴的其中一个交点1＜x2＜3，试比较m与n的大小，并说明理由．
分析 根据图象可得a＜0，b＞0，c=0，然后根据对称轴确定2a+b的符号，求m-n的值，判断差的符号即可．
解答 解：根据图象可得a＜0，b＞0，c=0．
则a-b＜0，0＜x=-$\frac{b}{2a}$＜1，则-b＞2a，即2a+b＜0，2a-b＜0，
当x=1是y=a+b+c=a+b＞0，
则m-n=|a-b|+|2a+b|-（|a+b|+|2a-b|）
=b-a-（2a+b）-（a+b）+（2a-b）
=b-a-2a-b-a-b+2a-b
=-2a-2b=-2（a+b）＜0，
则m＜n．
点评 本题考查了二次函数的图象的性质以及比较代数式的方法，一般转化为判断差的符号，正确去掉绝对值符号是关键．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
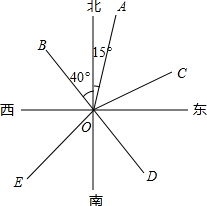如图，OA的方向是北偏东15°，OB的方向是北偏西40°．
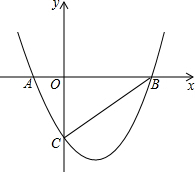如图，抛物线y=$\frac{\sqrt{3}}{2}$x2-$\frac{\sqrt{3}}{2}$x-$\sqrt{3}$与x轴相交于点A和点B，与y轴相交于点C，连接BC，在抛物线上找点D，连接CD，若∠BCD=90°，求点D的坐标．
根据几何体的三视图，画出它的展开图．
15．计算：a$\sqrt{b}$-c$\sqrt{b}$的结果是（ ）
| A． | a-c | B． | （a-c）$\sqrt{b}$ | C． | $\sqrt{{a}^{2}b}$-$\sqrt{{c}^{2}b}$ | D． | a-c$\sqrt{b}$ |
8．下列根式中，不能与$\sqrt{3}$合并的是（ ）
| A． | $\sqrt{\frac{1}{3}}$ | B． | $\frac{3}{{\sqrt{3}}}$ | C． | $\sqrt{\frac{2}{3}}$ | D． | $\sqrt{12}$ |
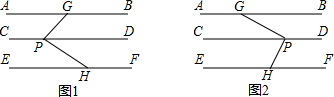
如图所示的几何体是由五个小正方形体组合而成的，它的俯视图是（ ）
