题目内容
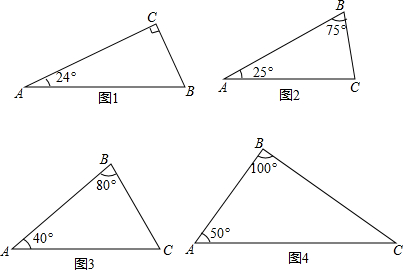
20.操作:(1)如图1中,∠C=90°,请用直尺和圆规作一条直线,把△ABC分割成两个等腰三角形(不写作法,但须保留作图痕迹).
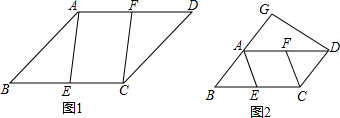
(2)已知内角度数的三个三角形如图2,图3,图4所示,请你判断,能否分别画一条直线把它们分割成两个等腰三角形?若能,请标出分割成的两个等腰三角形各角的度数;
(3)请你从上面两小题中获得的经验,猜想:任何三角形都能被分割成两个等腰三角形吗?一个三角形可以被分割成两个等腰三角形需满足什么条件?
分析 (1)如图1,作线段AB的垂直平分线得到AB的中点D,则DC=DA=DB,所以△DAC和△DBC都是等腰三角形;
(2)如图2,在∠ABC中作∠ABD=25°,则根据三角形内角和和等腰三角形的判定可得到△DAC和△DBC两个等腰三角形;在图3中,∠ACD=40°可得到两个等腰三角形;图4不能作;
(3)利用图1、图2、图3中三角形内角之间的关系进行判断.
解答 解:(1)如图1,CD为所作;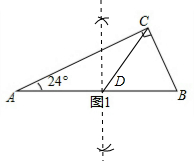
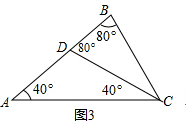
(2)图2、图3可以,图4不能.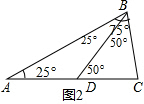
(3)三角形中有一个角为90°或有一个角是另一个角的3倍时,这个三角形可以被分割成两个等腰三角形.若有一个角是另一个角的2倍时,这个三角形不一定可以被分割成两个等腰三角形.
点评 本题考查了三角形综合题:熟练掌握三角形内角和和外角性质;理解等腰三角形的判定与性质;会作线段的垂直平分线.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
8.下列根式中,不能与$\sqrt{3}$合并的是( )
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\frac{3}{{\sqrt{3}}}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{12}$ |
5.下列根式中,能与$\sqrt{3}$合并的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{\frac{3}{2}}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{18}$ |
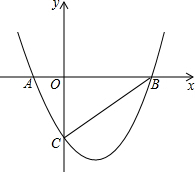 如图,抛物线y=$\frac{\sqrt{3}}{2}$x2-$\frac{\sqrt{3}}{2}$x-$\sqrt{3}$与x轴相交于点A和点B,与y轴相交于点C,连接BC,在抛物线上找点D,连接CD,若∠BCD=90°,求点D的坐标.
如图,抛物线y=$\frac{\sqrt{3}}{2}$x2-$\frac{\sqrt{3}}{2}$x-$\sqrt{3}$与x轴相交于点A和点B,与y轴相交于点C,连接BC,在抛物线上找点D,连接CD,若∠BCD=90°,求点D的坐标.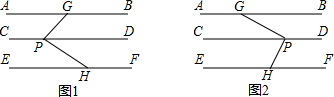
 如图所示的几何体是由五个小正方形体组合而成的,它的俯视图是( )
如图所示的几何体是由五个小正方形体组合而成的,它的俯视图是( )



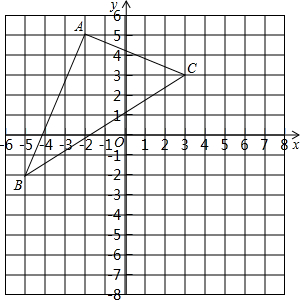 △ABC在平面直角坐标系xOy中的位置如图所示.
△ABC在平面直角坐标系xOy中的位置如图所示.