题目内容
16.已知:在平面直角坐标系中,M(0,1),N(2,2),在x轴上取一点P,使PM+PN的值最小,则点P的坐标为( )| A. | ($\frac{3}{2}$,0) | B. | (-$\frac{3}{2}$,0) | C. | (0,$\frac{3}{2}$) | D. | ($\frac{2}{3}$,0) |
分析 作出点M关于x轴的对称点M′,连接NM′交x轴于点P.由轴对称的性质可知MP+NP=M′P+NP,由两点之间线段最短可知:当M′、P、N在一条直线上时,MP+NP由最小值,然后求得直线M′N的解析式,最后令y=0即可求得点P的横坐标.
解答 解:如图所示:作出点M关于x轴的对称点M′,连接NM′交x轴于点P.
由轴对称的性质可知:MP=M′P,
∴MP+NP=M′P+NP.
由两点之间线段最短可知:当M′、P、N在一条直线上时,MP+NP由最小值.
设直线M′N所在直线的解析式为y=kx+b,
将点M′(0,-1)、N(2,2)代入得:$\left\{\begin{array}{l}{b=-1}\\{2k+b=2}\end{array}\right.$
解得:k=$\frac{3}{2}$,b=-1.
∴直线M′N的解析式为y=$\frac{3}{2}x-1$.
将y=0代入得;$\frac{3}{2}x-1=0$,
解得x=$\frac{2}{3}$.
∴点P的坐标为($\frac{2}{3}$,0)
故选:D.
点评 本题主要考查的是轴对称-路径最短问题、待定系数法求函数的解析式、一次函数与x轴的交点,明确M′、P、N在一条直线上时,MP+NP由最小值是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.用20cm长的绳子围成一个矩形,如果这个矩形的一边长为x cm,面积是S cm2,则S与x的函数关系式为( )
| A. | S=x(20-x) | B. | S=x(20-2x) | C. | S=10x-x2 | D. | S=2x(10-x) |
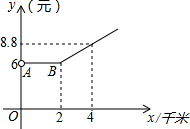 某市的出租车收费y(元)与路程x(千米)之间的函数关系如图所示.
某市的出租车收费y(元)与路程x(千米)之间的函数关系如图所示.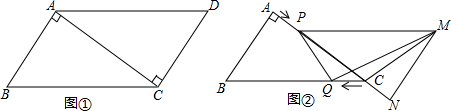
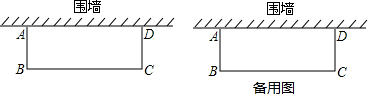
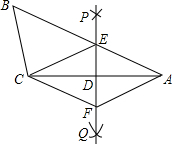 如图,已知△ABC,按如下步骤作图:
如图,已知△ABC,按如下步骤作图: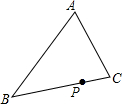 如图,点P在△ABC是边上一定点,请你找到一条过点P的直线,把△ABC分成面积相等的两部分,在图中画出这条直线并叙述画法:取AB中点D,过点D作DE∥AP交AB于点E,交AD与点H,连接EP,即为所求..
如图,点P在△ABC是边上一定点,请你找到一条过点P的直线,把△ABC分成面积相等的两部分,在图中画出这条直线并叙述画法:取AB中点D,过点D作DE∥AP交AB于点E,交AD与点H,连接EP,即为所求..