题目内容
8.教材第6页有一道题目:如图,矩形花圃一面靠墙(墙足够长),另外三面所围的栅栏的总长度是19m.(1)若花圃的面积是24m2,求AB边的长度是多少?
(2)若要围成的花圃面积最大,求这个最大值;
(3)若只利用这些栅栏将上题中这个矩形花圃分隔成两个有一边相邻的矩形花圃,且围成的总面积最大,求两个矩形花圃公共边的长.
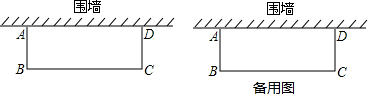
分析 (1)利用已知表示出BC的长,再利用矩形面积公式求出即可;
(2)利用矩形面积公式结合配方法求二次函数最值即可;
(3)根据题意表示出BC的长,进而利用二次函数性质得出即可.
解答 解:(1)设AB=x米,则BC=(19-2x)米,根据题意可得:
x(19-2x)=24,
解得:x1=8,x2=1.5.
答:AB边的长度是8米或1.5米;
(2)设围成的花圃面积为s,则
s=x(19-2x)=-2x2+19x=-2(x-$\frac{19}{4}$)2+$\frac{361}{8}$,
答:围成的花圃面积最大值是$\frac{361}{8}$m2;
(3)设垂直一边AD,分隔成两个有一边相邻的矩形花圃,
则这个矩形花圃分隔成两个有一边相邻的矩形花圃,则AB=x米,则BC=(19-3x)米,根据题意可得:
s=x(19-3x)=-3x2+19x,
当x=-$\frac{b}{2a}$=-$\frac{19}{2×(-3)}$=$\frac{19}{6}$时,围成的总面积最大,
此时BC=19-3×$\frac{19}{6}$=$\frac{19}{2}$(m),
故两个矩形花圃公共边的长为$\frac{19}{6}$m.
当平行AD分割后,此时公共边为$\frac{19}{4}$,最大面积为$\frac{361}{16}$m2,此时面积不是最大,舍去.
点评 此题主要考查了二次函数的应用以及一元二次方程的应用,根据题意正确表示出BC的长是解题关键.

练习册系列答案
相关题目
16.已知:在平面直角坐标系中,M(0,1),N(2,2),在x轴上取一点P,使PM+PN的值最小,则点P的坐标为( )
| A. | ($\frac{3}{2}$,0) | B. | (-$\frac{3}{2}$,0) | C. | (0,$\frac{3}{2}$) | D. | ($\frac{2}{3}$,0) |
20.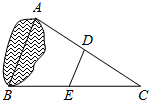 如图,A、B两地间有一池塘阻隔,为测量A、B两地的距离,在地面上选一点C,连接CA、CB的中点D、E,若DE的长度为30m,则A,B两地的距离是( )
如图,A、B两地间有一池塘阻隔,为测量A、B两地的距离,在地面上选一点C,连接CA、CB的中点D、E,若DE的长度为30m,则A,B两地的距离是( )
 如图,A、B两地间有一池塘阻隔,为测量A、B两地的距离,在地面上选一点C,连接CA、CB的中点D、E,若DE的长度为30m,则A,B两地的距离是( )
如图,A、B两地间有一池塘阻隔,为测量A、B两地的距离,在地面上选一点C,连接CA、CB的中点D、E,若DE的长度为30m,则A,B两地的距离是( )| A. | 15m | B. | 30m | C. | 60m | D. | 90m |
17.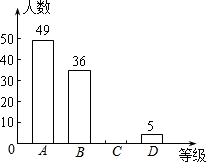 近年来,校园安全问题引起了社会的极大关注,为了让学生了解安全知识,增强安全意识,某校举行了一次“安全知识竞赛”.为了了解这次竞赛的成绩(取整数)情况,从中抽取了部分学生的成绩为一个样本,绘制了如下不完整统计图、表(说明:A级:90分-100分;B级:75分-89分;C级:60分-74分;D级:60分以下).
近年来,校园安全问题引起了社会的极大关注,为了让学生了解安全知识,增强安全意识,某校举行了一次“安全知识竞赛”.为了了解这次竞赛的成绩(取整数)情况,从中抽取了部分学生的成绩为一个样本,绘制了如下不完整统计图、表(说明:A级:90分-100分;B级:75分-89分;C级:60分-74分;D级:60分以下).
请结合统计图、表中提供的信息,解答下列问题:
(1)统计表中m=10,n=0.05,并把条形统计图补充完整.
(2)本次竞赛的中位数落在B级;
(3)若该校共有2000名学生,请你用此样本估计安全知识竞赛中A级和B级的学生共有多少人?
 近年来,校园安全问题引起了社会的极大关注,为了让学生了解安全知识,增强安全意识,某校举行了一次“安全知识竞赛”.为了了解这次竞赛的成绩(取整数)情况,从中抽取了部分学生的成绩为一个样本,绘制了如下不完整统计图、表(说明:A级:90分-100分;B级:75分-89分;C级:60分-74分;D级:60分以下).
近年来,校园安全问题引起了社会的极大关注,为了让学生了解安全知识,增强安全意识,某校举行了一次“安全知识竞赛”.为了了解这次竞赛的成绩(取整数)情况,从中抽取了部分学生的成绩为一个样本,绘制了如下不完整统计图、表(说明:A级:90分-100分;B级:75分-89分;C级:60分-74分;D级:60分以下).| 类别 | 频数 (人数) | 频率 |
| A | 49 | 0.49 |
| B | 36 | 0.36 |
| C | m | 0.1 |
| D | 5 | n |
(1)统计表中m=10,n=0.05,并把条形统计图补充完整.
(2)本次竞赛的中位数落在B级;
(3)若该校共有2000名学生,请你用此样本估计安全知识竞赛中A级和B级的学生共有多少人?
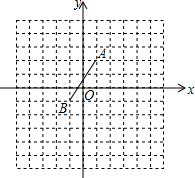 如图,在平面直角坐标系中,已知两点A(1,2),B(-1,-1),
如图,在平面直角坐标系中,已知两点A(1,2),B(-1,-1),
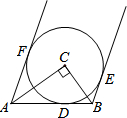 如图,在Rt△ABC中,∠C=90°,以点C为圆心作⊙C,与AB切于点D,过点A、B分别作⊙C的切线AF、BE,切点为F、E点.求证:AF∥BE.
如图,在Rt△ABC中,∠C=90°,以点C为圆心作⊙C,与AB切于点D,过点A、B分别作⊙C的切线AF、BE,切点为F、E点.求证:AF∥BE.