��Ŀ����
7����ͼ����һ��������ABCD����ƽ��ֱ������ϵ�У�AB=4��AD=2������ABƽ����x�ᣬADƽ����y�ᣬ��A������Ϊ��1��1������1����ֱ��д�����C������Ϊ��5��3����
��2����ͼ2����E�ڱ�CD�ϣ���DE=1���ѳ����ι���E�����۵����ۺ�ΪEF����B����B�䴦����C����C�䴦��ͼ�СϦ���Ϊ�۵��ǣ������۵���Ϊ���ٶ�ʱ��EC��ƽ����AD��д��������̣���ֱ��д����ʱ��F�����ꣻ
��3�������ֵ�E�ڱ�CD�ϣ���DE=1���ѳ����ι���E�����۵������۵������У����ۺ�EF�ѳ����ε������Ϊ1��3�������֣����F�����꣬д��������̣�
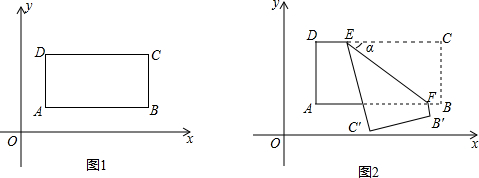
���� ��1�����ݾ��εij��ȣ�����ֱ����⣻
��2��EC��ƽ����AD�����CEC��=��D=90�㣬������á�a�Ķ�������F�����꼴����⣻
��3�����F��m��1����1��m��5�����ۺ�EF�ѳ����ε������Ϊ1��3�������֣���${S_{����ADEF}}=\frac{1}{3}{S_{����BCEF}}$��S����ADEF=3S����BCEF��������������ۣ����������ʽ�������з�����⣮
��� �⣨1��C��5��3����
��2����EC����ADʱ����CEC��=��D=90�㣬
���CEF=��C��EF=45�㣬
�����Ϧ�=45��ʱ��EC����AD��
��ʱ��F������Ϊ��3��1����
��3�����F��m��1����1��m��5��
��${S_{����ADEF}}=\frac{1}{3}{S_{����BCEF}}$ʱ��
$\frac{1}{2}��DE+AF��•AD=\frac{1}{6}��EC+BF��•BC$��
$\frac{1}{2}��1+m-1����2=\frac{1}{6}��5+5-m����2$��
��$m=\frac{5}{2}$��
��S����ADEF=3S����BCEFʱ��
$\frac{1}{2}��DE+AF��•AD=\frac{3}{2}��EC+BF��•BC$��$\frac{1}{2}��1+m-1����2=\frac{3}{2}��5+5-m����2$��
��$m=\frac{15}{2}��5$���������⣬��ȥ����
����$F��\frac{5}{2}��1��$���ۺ�EF�ѳ����ε������Ϊ1��3�������֣�
���� ���⿼����ͼ�ε��۵����Լ�ƽ���ı��ε����ʣ���ȷ�����۵������ʣ������۵��Ĺ����д��ڵ���ȵĽ��Լ���ȵ��߶��ǹؼ���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | -b6 | B�� | -b5 | C�� | b6 | D�� | b5 |

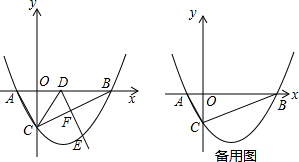
 ��ͼ���߳�Ϊ1�������κ�ֱ�DZ߳�Ϊ3�ĵ���ֱ�������Σ���ʼ��������ߺ��±��غϣ�����ֱ�������ι̶�����������������������ƽ��ֱ���Ƴ�������������ֹͣ�����������ƶ��ľ���Ϊx������ͼ���ص����Ϊy����y����x�ĺ���ͼ������ǣ�������
��ͼ���߳�Ϊ1�������κ�ֱ�DZ߳�Ϊ3�ĵ���ֱ�������Σ���ʼ��������ߺ��±��غϣ�����ֱ�������ι̶�����������������������ƽ��ֱ���Ƴ�������������ֹͣ�����������ƶ��ľ���Ϊx������ͼ���ص����Ϊy����y����x�ĺ���ͼ������ǣ�������



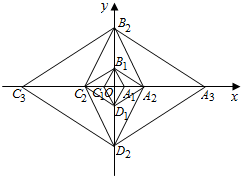 ��֪����A1B1C1D1�ı߳�Ϊ2����A1B1C1=60�㣬�Խ���A1C1��B1D1����ڵ�O���Ե�OΪ����ԭ�㣬�ֱ���OA1��OB1����ֱ��Ϊx�ᡢy�ᣬ������ͼ��ʾ��ֱ������ϵ����B1D1Ϊ�Խ���������B1C2D1A2������A1B1C1D1������A2C2Ϊ�Խ���������A2B2C2D2������B1C2D1A2������B2D2Ϊ�Խ���������B2C3D2A3������A2B2C2D2���������˹��ɼ�������ȥ����x����������ϵõ���A1��A2��A3������An�����An������Ϊ��3n-1��0����
��֪����A1B1C1D1�ı߳�Ϊ2����A1B1C1=60�㣬�Խ���A1C1��B1D1����ڵ�O���Ե�OΪ����ԭ�㣬�ֱ���OA1��OB1����ֱ��Ϊx�ᡢy�ᣬ������ͼ��ʾ��ֱ������ϵ����B1D1Ϊ�Խ���������B1C2D1A2������A1B1C1D1������A2C2Ϊ�Խ���������A2B2C2D2������B1C2D1A2������B2D2Ϊ�Խ���������B2C3D2A3������A2B2C2D2���������˹��ɼ�������ȥ����x����������ϵõ���A1��A2��A3������An�����An������Ϊ��3n-1��0����