题目内容

18．计算
（1）（-2ab2）2•（3a2b-2ab-1）；          
（2）（2a-b）2•（2a+b）2；
（3）（1+x-y）（x+y-1）；                
（4）9992-1002×998．

分析 （1）先算乘方，再按照单项式乘多项式的计算方法计算；
（2）（3）（4）先利用平方差公式计算，再利用完全平方公式计算即可．

解答 解：（1）（-2ab2）2•（3a2b-2ab-1）
=4a2b4•（3a2b-2ab-1）
=12a4b5-8a3b5-4a2b4；   
（2）（2a-b）2•（2a+b）2；
=[（2a-b）•（2a+b）]2
=（4a2-b2）2
=16a4+b4-8a2b2；
（3）（1+x-y）（x+y-1）
=[x+（1-y）][x-（1-y）]
=x2-（1-y）2
=x2-y2+2y-1；
（4）9992-1002×998
=9992-（1000+2）（1000-2）
=9992-10002+4
=（999+1000）（999-1000）+4
=-1999+4
=-1995．

点评 此题考查整式的混合运算，掌握计算方法和计算公式是解决问题的关键．

练习册系列答案
相关题目
7．如图，已知AB是⊙O的直径，点C在⊙O上，若∠CAB=40°，则∠ABC的度数为50°．
9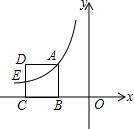．如图，正方形ABCD的边BC在x轴的负半轴上，其中E是CD的中点，函数y=$\frac{k}{x}$的图象经过点A、E．若B点的坐标是（-3，0），则k的值为（　　）
A．-5B．-4C．-6D．-9
6．若8x=4x+2，则x=4．
13．计算：
（1）$\frac{1}{a-1}-\frac{a}{a-1}$
（2）$\frac{{a}^{2}}{{a}^{2}+2a}$•（$\frac{{a}^{2}}{a-2}$-$\frac{4}{a-2}$）
3．在△ABC中，已知点D、E、F分别是边BC、AD、CE上的中点，且S△ABC=4cm2，则S△BEF的值为（　　）
A．2cm2B．1cm2C．0.5cm2D．0.25cm2
10．阅读下面材料，然后解答问题：
材料：（a+b）（a2-ab+b2）=a•a2-a•ab+a•b2+b•a2-b•ab+b•b2，于是合并后可得（a+b）（a2-ab+b2）=a3+b3，
（1）将下列多项式进行因式分解：x3+8y3=（x+2y）（x2-2xy+4y2）
（2）应用：有趣的“约分”$\frac{{{3^3}+{1^3}}}{{{3^3}+{2^3}}}=\frac{3+1}{3+2}$，$\frac{{5^3+{2^3}}}{{{5^3}+{3^3}}}=\frac{5+2}{5+3}$，$\frac{{{6^3}+{2^3}}}{{{6^3}+{4^3}}}=\frac{6+2}{6+4}$，$\frac{{{7^3}+{4^3}}}{{{7^3}+{3^3}}}=\frac{7+4}{7+3}$…
面对这样荒谬的“约分”，一笑之后，再认真检查，发现其结果竟然正确；
仔细观察式子，完成以下问题：
①$\frac{1{0}^{3}+{1}^{3}}{（）}$=$\frac{（）}{（）}$，
②猜想：$\frac{{a}^{3}+{b}^{3}}{（）}$=$\frac{（）}{（）}$
③你能证明你的猜想吗？
7．如图，把一个长方形ABCD放在平面直角坐标系中，AB=4，AD=2，其中AB平行于x轴，AD平行于y轴，点A的坐标为（1，1）．
（1）请直接写出求点C的坐标为（5，3）；
（2）如图2，点E在边CD上，且DE=1，把长方形过点E进行折叠，折痕为EF，点B落在B′处，点C落在C′处，图中∠α称为折叠角，试问折叠角为多少度时，EC′平行于AD，写出计算过程，并直接写出此时点F的坐标；
（3）若保持点E在边CD上，且DE=1，把长方形过点E进行折叠，在折叠过程中，若折痕EF把长方形的面积分为1：3的两部分，求点F的坐标，写出计算过程．
8．已知实数x1，x2满足x1+x2=7，x1x2=12，则以x1，x2为根的一元二次方程是（　　）
A．x2-7x+12=0B．x2+7x+12=0C．x2+7x-12=0D．x2-7x-12=0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网