题目内容
17．已知（m-1）2+|n+2|=0，求代数式-（m2-2mn）•12m2-（12m•n3+8m4•n2）÷4mn的值．分析 先求出m、n的值，再算乘法和除法，合并同类项，最后代入求出即可．
解答 解：∵（m-1）2+|n+2|=0，
∴m-1=0，n+2=0，
∴m=1，n=-2，
∴-（m2-2mn）•12m2-（12m•n3+8m4•n2）÷4mn
=-12m4+24m3n-3n2-2m3n
=-12m4+22m3n-3n2
=-12×14+22×13×（-2）-3×（-2）2
=-68．
点评 本题考查了整式的混合运算和求值的应用，能运用整式的混合运算法则进行化简是解此题的关键，难度适中．
练习册系列答案
金钥匙试卷系列答案
相关题目
8．已知实数x1，x2满足x1+x2=7，x1x2=12，则以x1，x2为根的一元二次方程是（ ）
| A． | x2-7x+12=0 | B． | x2+7x+12=0 | C． | x2+7x-12=0 | D． | x2-7x-12=0 |
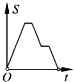
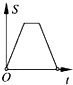
如图，在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG，动点P从点A出发，沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止（不含点A和点B），则△ABP的面积S随着时间t变化的函数图象大致是（ ）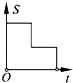
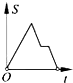
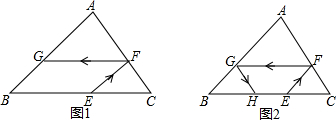
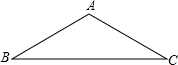如图，△ABC是等腰三角形，AB=AC，请你用尺规作图将△ABC分成两个全等的三角形，并说明这两个三角形全等的理由．（保留作图痕迹，不写作法）