题目内容
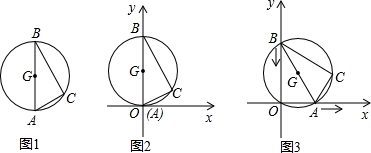
11. 如图,某数学兴趣小组将一段长为4的铁丝,围成以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形的最大面积为1.
如图,某数学兴趣小组将一段长为4的铁丝,围成以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形的最大面积为1.
分析 设半径长是x,则弧长是4-2x,利用扇形的面积公式即可把面积用x表示,利用二次函数的性质即可求解.
解答 解:设半径长是x,则弧长是4-2x.
则扇形的面积s=$\frac{1}{2}$x(4-2x),
即S=-x2+2x=-(x2-2x+1)+1=-(x-1)2+1.
则扇形的面积是最大值是1.
故答案是1.
点评 本题考查了扇形的面积和二次函数的性质,正确列出函数解析式是关键.

练习册系列答案
相关题目
19.若函数y=(m-1)x2+3x+1是二次函数,则有( )
| A. | m≠0 | B. | m≠1 | C. | x≠0 | D. | x≠1 |
6.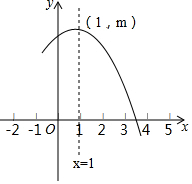 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,m),且与x轴的一个交点在点(3,0)和(4,0)之间,下列结论错误的是( )
如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,m),且与x轴的一个交点在点(3,0)和(4,0)之间,下列结论错误的是( )
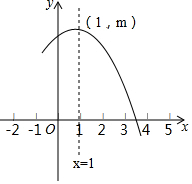 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,m),且与x轴的一个交点在点(3,0)和(4,0)之间,下列结论错误的是( )
如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,m),且与x轴的一个交点在点(3,0)和(4,0)之间,下列结论错误的是( )| A. | a-b+c>0 | |
| B. | b2=4a(c-m) | |
| C. | 2a+c<0 | |
| D. | 一元二次方程ax2+bx+c=m-1有两个不相等的实数根 |
20.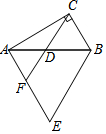 如图,在△ABC中,∠ACB=90°,∠CBA=60°.△ABE是等边三角形,D是AB的中点,连接CD并延长,交AE于点F.若CD=2,则EF的长为( )
如图,在△ABC中,∠ACB=90°,∠CBA=60°.△ABE是等边三角形,D是AB的中点,连接CD并延长,交AE于点F.若CD=2,则EF的长为( )
 如图,在△ABC中,∠ACB=90°,∠CBA=60°.△ABE是等边三角形,D是AB的中点,连接CD并延长,交AE于点F.若CD=2,则EF的长为( )
如图,在△ABC中,∠ACB=90°,∠CBA=60°.△ABE是等边三角形,D是AB的中点,连接CD并延长,交AE于点F.若CD=2,则EF的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | $\frac{3}{2}$ |
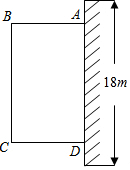 为了改善小区环境,某小区决定要在一块一边靠墙(墙长18m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图),设绿化带BC边长为xm,绿化带的面积为ym2.
为了改善小区环境,某小区决定要在一块一边靠墙(墙长18m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图),设绿化带BC边长为xm,绿化带的面积为ym2.