题目内容
3.下列结论中正确的个数有( )(1)$\sqrt{6m({a^2}+{b^2}})$不是最简二次根式; (2)$\sqrt{8a}$与$\sqrt{\frac{1}{2a}}$是同类二次根式;(3)$\sqrt{a}$与$\sqrt{a}$互为有理化因式; (4)(x-1)(x+2)=x2是一元二次方程.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 依据最简二根式的定义可对(1)作出判断;依据同类二次根式的定义可对(2)作出判断,依据两个二次根式的乘积是否为整式可对(3)作出判断;(4)先化简,然后依据一元二次根式的定义进行判断即可.
解答 解:(1)$\sqrt{6m({a^2}+{b^2}})$是最简二次根式,故(1)错误;
(2)$\sqrt{8a}$与$\sqrt{\frac{1}{2a}}$是同类二次根式,故(2)正确;
(3)$\sqrt{a}$与$\sqrt{a}$互为有理化因式,故(3)正确;
(4)方程(x-1)(x+2)=x2整理得:x-2=0,故(4)错误.
故选:C.
点评 本题主要考查的是最简二次根式、同类二次根式、有理化因式、一元二次方程的定义,熟练掌握相关知识是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.解不等式(组)$\left\{\begin{array}{l}{2(1-x)≤x-10}\\{\frac{3x+14}{4}>2x-9}\end{array}\right.$,并写出它的整数解.
15.若a<b,则下列不等式成立的是( )
| A. | ma<mb | B. | 2a>2b | C. | -2a>-2b | D. | $\frac{a}{2}$>$\frac{b}{2}$ |
12.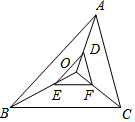 如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )
如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )
 如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )
如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
13.已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2009的值为( )
| A. | (-3)2009 | B. | -1 | C. | 0 | D. | 1 |
 如图,某数学兴趣小组将一段长为4的铁丝,围成以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形的最大面积为1.
如图,某数学兴趣小组将一段长为4的铁丝,围成以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形的最大面积为1. 如图,矩形ABCD中,以AB为直径作⊙O,点E是CD的中点,连接BE交⊙O于点F,连接DF并延长交BC于点G.
如图,矩形ABCD中,以AB为直径作⊙O,点E是CD的中点,连接BE交⊙O于点F,连接DF并延长交BC于点G.