题目内容
16．
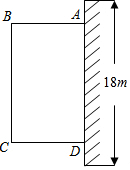为了改善小区环境，某小区决定要在一块一边靠墙（墙长18m）的空地上修建一个矩形绿化带ABCD，绿化带一边靠墙，另三边用总长为40m的栅栏围住（如图），设绿化带BC边长为xm，绿化带的面积为ym2．（1）求y与x之间的函数关系式，并写出自变量x的取值范围；
（2）绿化带的面积能不能为200m2？如果能，求出x的值；如果不能，请说明理由．
分析 （1）根据题意可以列出y与x之间的函数关系式并写出x的取值范围；
（2）先判断绿化带的面积能不能为200m2，然后说明理由即可解答本题．
解答 解：（1）由题意可得，
y=x•$\frac{40-x}{2}$=$-\frac{1}{2}{x}^{2}+20x$，
即y与x之间的函数关系式是y=$-\frac{1}{2}{x}^{2}+20x$（0＜x≤18）；
（2）绿化带的面积不能为200m2，
理由：将y=200代入y=$-\frac{1}{2}{x}^{2}+20x$，
得200=$-\frac{1}{2}{x}^{2}+20x$，
解得，x=20，
∵20＞18，
∴绿化带的面积不能为200m2．
点评 本题考查二次函数的应用、一元二次方程的应用，解答本题的关键是明确题意，列出相应的函数和一元二次方程．
练习册系列答案
相关题目
6．点（a-2，b+2）经过平移变换得到点（a，b），则这个平移变换是（ ）
| A． | 先向左平移2个单位长度，再向下平移2个单位长度 | |
| B． | 先向左平移2个单位长度，再向上平移2个单位长度 | |
| C． | 先向右平移2个单位长度，再向下平移2个单位长度 | |
| D． | 先向右平移2个单位长度，再向上平移2个单位长度 |
4．小红和其他2名同学排成一排拍照，则小红排在正中间的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
如图，某数学兴趣小组将一段长为4的铁丝，围成以A为圆心，AB为半径的扇形（忽略铁丝的粗细），则所得扇形的最大面积为1．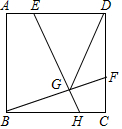
如图，正方形ABCD中，点E在边AD上，点F在边CD上，AE=CF，EH⊥BF于点G，连接DG．
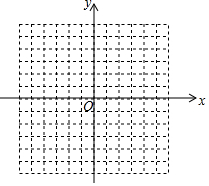如图，方格纸中每个小正方形的边长都是单位1，△ABC的三个顶点都在格点（即这些小正方形的顶点）上，且它们的坐标分别是A（2，-3），B（5，-1），C（-1，3），结合所给的平面直角坐标系，解答下列问题：
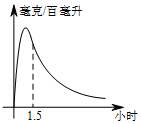实验数据显示：一般成人喝半斤低度白酒后，1.5小时内（包括1.5小时）其血液中酒精含量y（毫克/百毫升）与时间x（时）的关系可近似地用二次函数y=-200x2+400x表示，1.5小时后（包括1.5小时）y与x可近似地用反比例函数y=$\frac{k}{x}$（k＞0）表示（如图所示）