Question

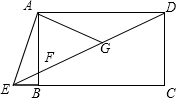如图，四边形ABCD是矩形，点E在线段CB的延长线上，连接DE交AB于点F，∠AED=2∠CED，点G是DF的中点．若BE=2，AG=8，则AB的长为

 

．

Answer 1

考点：勾股定理,等腰三角形的判定与性质,直角三角形斜边上的中线,矩形的性质

专题：

分析：根据直角三角形斜边上的中线等于斜边的一半可得AG=DG，然后根据等边对等角的性质可得∠ADG=∠DAG，再结合两直线平行，内错角相等可得∠ADG=∠CED，再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠AGE=2∠ADG，从而得到∠AED=∠AGE，再利用等角对等边的性质得到AE=AG，然后利用勾股定理列式计算即可得解．

解答：解：∵四边形ABCD是矩形，点G是DF的中点，
∴AG=DG，
∴∠ADG=∠DAG，
∵AD∥BC，
∴∠ADG=∠CED，
∴∠AGE=∠ADG+∠DAG=2∠CED，
∵∠AED=2∠CED，
∴∠AED=∠AGE，
∴AE=AG=8，
在Rt△ABE中，AB=

AE2-BE2

=

82-22

=2

15

．
故答案为：2

15

．

点评：本题考查了矩形的性质，等边对等角的性质，等角对等边的性质，以及勾股定理的应用，求出AE=AG是解题的关键．