题目内容
若一个直角三角形的两边长分别是2、4，则第三边长为 ．
考点：勾股定理
专题：分类讨论
分析：本题已知直角三角形的两边长，但未明确这两条边是直角边还是斜边，所以求第三边的长必须分类讨论，即4是斜边或直角边的两种情况，然后利用勾股定理求解．
解答：解：设第三边为x
若4是直角边，则第三边x是斜边，由勾股定理，得22+42=x2，解得x=2
；
若4是斜边，则第三边x为直角边，由勾股定理，得22+x2=42，解得x=2
．
所以第三边的长为2
或2
．
故答案为：2
或2
．
若4是直角边，则第三边x是斜边，由勾股定理，得22+42=x2，解得x=2
| 5 |
若4是斜边，则第三边x为直角边，由勾股定理，得22+x2=42，解得x=2
| 3 |
所以第三边的长为2
| 5 |
| 3 |
故答案为：2
| 5 |
| 3 |
点评：本题考查的是勾股定理，在解答此题是时要注意分类讨论，不要漏解．
练习册系列答案
相关题目
如图，矩形ABCD的面积为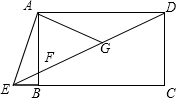
如图，四边形ABCD是矩形，点E在线段CB的延长线上，连接DE交AB于点F，∠AED=2∠CED，点G是DF的中点．若BE=2，AG=8，则AB的长为下列二次根式中，是最简二次根式的是（ ）
A、2
| ||||
B、
| ||||
C、
| ||||
D、
|