题目内容
一个n边形的内角和是540°，那么n= ．
考点：多边形内角与外角
专题：
分析：根据n边形的内角和为（n-2）•180°得到（n-2）•180°=540°，然后解方程即可．
解答：解：设这个多边形的边数为n，由题意，得
（n-2）•180°=540°，
解得n=5．
故答案为：5．
（n-2）•180°=540°，
解得n=5．
故答案为：5．
点评：本题考查了多边的内角和定理：n边形的内角和为（n-2）•180°．
练习册系列答案
活力课时同步练习册系列答案
相关题目
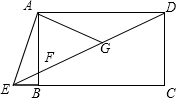如图，四边形ABCD是矩形，点E在线段CB的延长线上，连接DE交AB于点F，∠AED=2∠CED，点G是DF的中点．若BE=2，AG=8，则AB的长为若正六边形的边长为a，则其外接圆半径与内切圆半径的比为（ ）
| A、2：1 | ||
B、2：
| ||
C、
| ||
D、3：
|