题目内容
12．
如图，在△ABC中，D、E、F分别是AB，BC，AC上的点，且DE∥AC，EF∥BA，FD∥CB．试说明：E是线段BC的中点．
分析 根据DE∥AC，FD∥CB，证得四边形DECF是平行四边形，于是得到DF=CE，根据EF∥BA，FD∥CB，证得四边形DBEF是平行四边形，于是得到DF=BE，等量代换得到BE=CE，于是得到结论．
解答 证明：∵DE∥AC，FD∥CB，
∴四边形DECF是平行四边形，
∴DF=CE，
∵EF∥BA，FD∥CB，
∴四边形DBEF是平行四边形，
∴DF=BE，
∴BE=CE，
∴E是线段BC的中点．
点评 本题考查了平行四边形的判定和性质，熟练掌握平行四边形的判定和性质是解题的关键．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
如图，在矩形ABCD中，AC、BD相交于O，AE平分∠BAD，交BC于E，若∠CAE=15°，求∠OBE的度数．
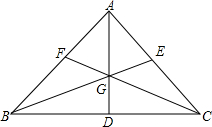如图在△ABC中，点D、E、F分别在三边上，E是AC中点．AD、BE、CF交于点G，BD=2DC，S△GCE=4，S△GCD=5，求△ABC的面积？