题目内容

4．若一个凸四边形的内角和与外角和相等，那么它是四边形．

分析 由任意多边形的外角和为360°可求得它的内角和为360°，然后根据多边形的内角公式求解即可．

解答 解：设多边形的边数为n．
根据题意得：（n-2）×180°=360°．
解得：n=4．
故答案为：四．

点评 本题主要考查的是多边形的内角和与外角和，掌握多边形的内角和公式、外角和定理是解题的关键．

练习册系列答案
相关题目
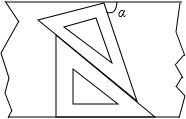14．如图，一副三角板放置在两边互相平行的纸板上，其中下面部分是含45°角的三角板上，上面部分是一个含30°角的三角板，则图中∠α的度数是75°．
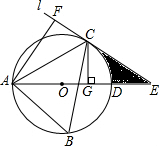15．如图，△ABC内接于⊙O，过点C作圆的切线l与直径AD的延长线交于点E，AF⊥l，垂足为F，CG⊥AD，垂足为G．
（1）求证：△ACF≌△ACG；
（2）若∠B=60°，AF=4，求图中阴影部分的面积．
12．如图，在△ABC中，D、E、F分别是AB，BC，AC上的点，且DE∥AC，EF∥BA，FD∥CB．试说明：E是线段BC的中点．
19．关于x的方程kx2+（k+2）x+$\frac{k}{4}$=0有两个不相等的实数根
（1）求k的取值范围；
（2）当k=4时方程的两根分别为x1、x2，直接写出x1+x2，x1x2的值；
（3）是否存在实数k使方程的两个实数根的倒数和等于0？若存在，求出k的值；若不存在，说明理由．
9．已知：线段AB，BC，∠ABC=90°．求作：矩形ABCD．以下是甲、乙两同学的作业：

请分别判断上述两人的作业是否正确并说明理由．
16．已知一个两位数，其个位上的数为x，十位上的数比个位上的数大1，则这个两位数可表示为（　　）
A．11x-1B．11x-10C．11x+1D．11x+10
13．若9x2-（k+1）x+4是完全平方式，则k的值为（　　）
A．±11B．11或-13C．11D．-11
14．甲、乙两个家庭同去一家粮店购买大米两次．两次大米的售价有变化，但两个家庭的购买方式不同，其中甲家庭每次总是买20千克大米，而乙家庭每次用去20元，商店也按价计算卖给乙家庭．设前后两次的米价分别是每千克m元和n元（m＞0，n＞0，m≠n），请问谁的购买方式合算？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网