题目内容
2.分解因式:x2-11xy+3y2.分析 根据完全平方公式,可得平方差公式,根据平方差公式,可得答案.
解答 解:原式=[x2-11x+($\frac{11}{2}$y)2]-($\frac{\sqrt{109}}{2}$y)2
=(x-$\frac{11}{2}$y)2-($\frac{\sqrt{109}}{2}$y)2
=[(x-$\frac{11}{2}$y)+$\frac{\sqrt{109}}{2}$y][(x-$\frac{11}{2}$y)-$\frac{\sqrt{109}}{2}$y]
=[x-($\frac{11}{2}$-$\frac{\sqrt{109}}{2}$)y][x-($\frac{11}{2}$+$\frac{\sqrt{109}}{2}$)y].
点评 本题考查了因式分解,利用了完全平方公式、平方差公式分解因式,注意分解要彻底.

练习册系列答案
相关题目
7. 如图,在平面直角坐标系中,直线CD与x轴、y轴分别交于点C,D,与反比例函数y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于E,F.过点E作EA⊥y轴于A,过点F作FB⊥x轴于B,直线EA与FB交于点G.若$\frac{DE}{DF}$=$\frac{1}{4}$,记△GEF的面积为S1,△OEF的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,在平面直角坐标系中,直线CD与x轴、y轴分别交于点C,D,与反比例函数y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于E,F.过点E作EA⊥y轴于A,过点F作FB⊥x轴于B,直线EA与FB交于点G.若$\frac{DE}{DF}$=$\frac{1}{4}$,记△GEF的面积为S1,△OEF的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
 如图,在平面直角坐标系中,直线CD与x轴、y轴分别交于点C,D,与反比例函数y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于E,F.过点E作EA⊥y轴于A,过点F作FB⊥x轴于B,直线EA与FB交于点G.若$\frac{DE}{DF}$=$\frac{1}{4}$,记△GEF的面积为S1,△OEF的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,在平面直角坐标系中,直线CD与x轴、y轴分别交于点C,D,与反比例函数y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于E,F.过点E作EA⊥y轴于A,过点F作FB⊥x轴于B,直线EA与FB交于点G.若$\frac{DE}{DF}$=$\frac{1}{4}$,记△GEF的面积为S1,△OEF的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{1}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{8}$ |
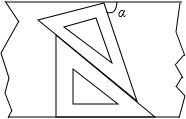 如图,一副三角板放置在两边互相平行的纸板上,其中下面部分是含45°角的三角板上,上面部分是一个含30°角的三角板,则图中∠α的度数是75°.
如图,一副三角板放置在两边互相平行的纸板上,其中下面部分是含45°角的三角板上,上面部分是一个含30°角的三角板,则图中∠α的度数是75°. 如图,在△ABC中,D、E、F分别是AB,BC,AC上的点,且DE∥AC,EF∥BA,FD∥CB.试说明:E是线段BC的中点.
如图,在△ABC中,D、E、F分别是AB,BC,AC上的点,且DE∥AC,EF∥BA,FD∥CB.试说明:E是线段BC的中点.