题目内容
3. 如图,在矩形ABCD中,AC、BD相交于O,AE平分∠BAD,交BC于E,若∠CAE=15°,求∠OBE的度数.
如图,在矩形ABCD中,AC、BD相交于O,AE平分∠BAD,交BC于E,若∠CAE=15°,求∠OBE的度数.
分析 先根据AE平分∠BAD交BC于E可得∠AEB=45°,再根据三角形的外角性质求出∠ACB=30°,然后判断出△AOB是等边三角形,从而可以得出△BOE是等腰三角形,然后根据三角形的内角和是180°进行求解即可.
解答 解:∵AE平分∠BAD交BC于E,
∴∠BAE=45°,AB=BE,
∵∠CAE=15°,
∴∠BAO=60°,
又∵OA=OB,
∴△BOA是等边三角形,
∴∠ABO=60°,
∴∠OBE=30°.
点评 本题考查了矩形的性质,等边三角形的判定及性质,求出∠BAO=60°,然后判断出等边三角是解本题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
13.若9x2-(k+1)x+4是完全平方式,则k的值为( )
| A. | ±11 | B. | 11或-13 | C. | 11 | D. | -11 |
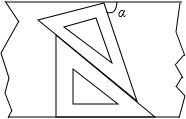 如图,一副三角板放置在两边互相平行的纸板上,其中下面部分是含45°角的三角板上,上面部分是一个含30°角的三角板,则图中∠α的度数是75°.
如图,一副三角板放置在两边互相平行的纸板上,其中下面部分是含45°角的三角板上,上面部分是一个含30°角的三角板,则图中∠α的度数是75°. 如图,已知:AB∥CD,∠B+∠D=180°,BC与DE有何位置关系?并说明理由.
如图,已知:AB∥CD,∠B+∠D=180°,BC与DE有何位置关系?并说明理由.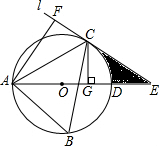 如图,△ABC内接于⊙O,过点C作圆的切线l与直径AD的延长线交于点E,AF⊥l,垂足为F,CG⊥AD,垂足为G.
如图,△ABC内接于⊙O,过点C作圆的切线l与直径AD的延长线交于点E,AF⊥l,垂足为F,CG⊥AD,垂足为G. 如图,在△ABC中,D、E、F分别是AB,BC,AC上的点,且DE∥AC,EF∥BA,FD∥CB.试说明:E是线段BC的中点.
如图,在△ABC中,D、E、F分别是AB,BC,AC上的点,且DE∥AC,EF∥BA,FD∥CB.试说明:E是线段BC的中点.