题目内容
已知:AB为⊙O的弦,半径OD所在直线垂直AB于C,若AB=2
厘米,OC=1厘米,求CD的长.
| 3 |
考点:垂径定理,勾股定理
专题:
分析:如图,连接OA.由垂径定理推知AC=
AB=
厘米,在直角△AOC中利用勾股定理求得OA=2,所以CD=OD-OC=OA-OC.
| 1 |
| 2 |
| 3 |
解答: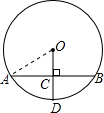 解:如图,连接OA.
解:如图,连接OA.
∵AB为⊙O的弦,半径OD所在直线垂直AB于C,AB=2
厘米,
∴AC=
AB=
厘米.
又∵OC=1厘米,
∴在直角△AOC中,由勾股定理得到:OA=
=2厘米,
∴CD=OA-OC=1厘米.
 解:如图,连接OA.
解:如图,连接OA.∵AB为⊙O的弦,半径OD所在直线垂直AB于C,AB=2
| 3 |
∴AC=
| 1 |
| 2 |
| 3 |
又∵OC=1厘米,
∴在直角△AOC中,由勾股定理得到:OA=
| AC2+OC2 |
∴CD=OA-OC=1厘米.
点评:本题考查了圆周角定理、勾股定理.此题涉及圆中求半径的问题,此类在圆中涉及弦长、半径、圆心角的计算的问题,常把半弦长,半圆心角,圆心到弦距离转换到同一直角三角形中,然后通过直角三角形予以求解.

练习册系列答案
相关题目
关于x的一元二次方程x2-(m+n)x+mn=0的根的情况是( )
| A、有两个相等的实数根 |
| B、有两个不相等实数根 |
| C、有两个实数根 |
| D、没有实数根 |
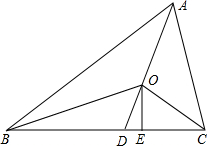 如图,O是△ABC的三内角平分线的交点,OE⊥BC.
如图,O是△ABC的三内角平分线的交点,OE⊥BC.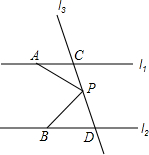 如图,已知直线l1∥l2,直线l3和直线l1,l2交于点C和D,点P在直线l3上,
如图,已知直线l1∥l2,直线l3和直线l1,l2交于点C和D,点P在直线l3上, 在?ABCD中,E,F为BD上的点,BF=DE,求证:四边形AECF是平行四边形.
在?ABCD中,E,F为BD上的点,BF=DE,求证:四边形AECF是平行四边形.