Question

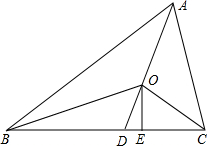如图，O是△ABC的三内角平分线的交点，OE⊥BC．
（1）若∠BAC=60°，∠ACB=80°，则∠BOD=

 

，∠EOC=

 

；
（2）试猜想∠BOD与∠EOC之间的大小关系，并证明你的结论．

Answer 1

考点：三角形内角和定理

专题：

分析：（1）根据角平分线求出∠BAO和∠ABO，根据三角形外角性质求出∠BOD即可，求出∠OCB，根据三角形内角和定理求出∠EOC即可；
（2）根据角平分线求出∠ABO=

1

2

∠ABC，∠BAO=

1

2

∠BAC，∠OCB=

1

2

∠ACB，根据三角形内角和定理和三角形外角性质求出即可．

解答：解：（1）∵∠BAC=60°，∠ACB=80°，O是△ABC的三内角平分线的交点，
∴∠BAD=

1

2

∠BAC=30°，∠ABC=180°-∠BAC-∠ACB=40°，
∴∠ABO=

1

2

∠ABC=20°，
∴∠BDO=∠BAO+∠ABO=30°+20°=50°，
∵∠ACB=80°，CO平分∠ACB，
∴∠OCB=

1

2

∠ACB=40°，
∵OE⊥BC，
∴∠OEC=90°，
∴∠EOC=90°-40°=50°，
故答案为：50°，50°．

（2）∠BOD=∠EOC，
∵O是△ABC的三内角平分线的交点，
∴∠ABO=

1

2

∠ABC，∠BAO=

1

2

∠BAC，∠OCB=

1

2

∠ACB，
∵∠BAC+∠ABC+∠ACB=180°，
∴∠BAC+∠ABC=180°-∠ACB，
∴∠BOD=∠BAO+∠ABO=

1

2

（∠BAC+∠ABC）=

1

2

（180°-∠ACB）=90°-

1

2

∠ACB，
∵∠OEC=90°，∠OCB=

1

2

∠ACB，
∴∠EOC=90°-

1

2

∠ACB，
即∠BOD=∠EOC．

点评：本题主要考查三角形内角平分线的性质及三角形内角和定理的推论，三角形外角性质的应用，主要考查学生的推理能力和计算能力．