题目内容
关于x的一元二次方程x2-（m+n）x+mn=0的根的情况是（ ）
| A、有两个相等的实数根 |
| B、有两个不相等实数根 |
| C、有两个实数根 |
| D、没有实数根 |
考点：根的判别式
专题：
分析：根据△=b2-4ac=[-（m+n）]2-4×1×mn，再判断出△的符号，即可得出答案．
解答：解：∵△=[-（m+n）]2-4×1×mn=m2+n2-2mn=（m-n）2≥0，
∴方程有两个实数根；
故选C．
∴方程有两个实数根；
故选C．
点评：本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
练习册系列答案
相关题目
把一枚质地均匀的普通硬币掷一次，落地后正面朝上的概率是（ ）
A、
| ||
| B、1 | ||
C、
| ||
D、
|
|
| A、0 | B、4 | C、-4 | D、2 |
一元二次方程x2-kx-1=0的根的情况是（ ）
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、没有实数根 |
| D、无法判断 |
抛物线y=x2-8x+15的顶点坐标为（ ）
| A、（4，-1） |
| B、（0，-3） |
| C、（-2，-3） |
| D、（-2，-1） |
如图：OA⊥OB，∠BOC=20°，OD平分∠AOC，则∠BOD的度数是（ ）| A、45° | B、40° |
| C、35° | D、30° |
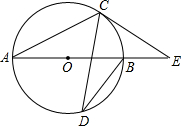如图，AB是⊙O的直径，C、D是⊙O上一点，∠CDB=25°，过点C作⊙O的切线交AB的延长线于点E，则∠E等于（ ）| A、35° | B、40° |
| C、45° | D、50° |
下列图案中，不是中心对称图形的是（ ）
A、 |
B、 |
C、 |
D、 |