题目内容
1.已知a,b,c,d满足a<-1<b<0<c<1<d,且|a+1|=|b+1|,|1-c|=|1-d|,那么a+b+c+d=0.分析 根据已知不等式确定出绝对值里边式子的正负,已知等式利用绝对值的代数意义化简,整理求出a+b与c+d的值,代入原式计算即可得到结果.
解答 解:∵a<-1<b<0<c<1<d,
∴a+1<0,b+1>0,1-c>0,1-d<0,
∵|a+1|=|b+1|,|1-c|=|1-d|,
∴-a-1=b+1,1-c=d-1,
整理得:a+b=-2,c+d=2,
则a+b+c+d=0.
故答案为:0
点评 此题考查了绝对值,熟练掌握绝对值的代数意义是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.若a与b互为相反数,则|a+b-2|等于( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
11.正比例函数y=x的图象与反比例函数y=$\frac{1}{x}$的图象的交点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第一、三象限 |
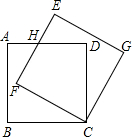 如图,边长为10的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长为$\frac{10\sqrt{3}}{3}$.
如图,边长为10的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长为$\frac{10\sqrt{3}}{3}$.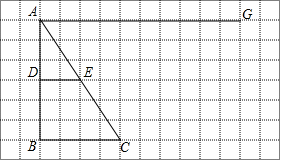 如图,在网格图中,有△ABC与线段DE,在线段AG上是否存在点M,使得△MEC与△ADE相似?若存在,请先在图中确定出所有的点M,并选择其中一个说明理由;若不存在,也请说明理由.(图中各点均在格点上).
如图,在网格图中,有△ABC与线段DE,在线段AG上是否存在点M,使得△MEC与△ADE相似?若存在,请先在图中确定出所有的点M,并选择其中一个说明理由;若不存在,也请说明理由.(图中各点均在格点上).