题目内容
11．正比例函数y=x的图象与反比例函数y=$\frac{1}{x}$的图象的交点位于（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第一、三象限 |
分析 联立两函数解析式成方程组，解之即可得出交点坐标，由此即可得出结论．
解答 解：联立两函数解析式成方程组，$\left\{\begin{array}{l}{y=x}\\{y=\frac{1}{x}}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=1}\end{array}\right.$，$\left\{\begin{array}{l}{{x}_{2}=-1}\\{{y}_{2}=-1}\end{array}\right.$．
∴正比例函数y=x的图象与反比例函数y=$\frac{1}{x}$的图象的交点位于第一、三象限．
故选D．
点评 本题考查了反比例函数与一次函数的交点问题，联立两函数解析式成方程组，通过解方程组即可求出交点坐标．
练习册系列答案
相关题目
2．
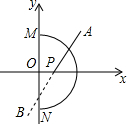如图，在平面直角坐标系中，以原点O为圆心，3为半径的半圆，直线AB：y=x+b与x轴交于点P（x，0），若直线AB与半圆弧有公共点，则x值的范围是（ ）
如图，在平面直角坐标系中，以原点O为圆心，3为半径的半圆，直线AB：y=x+b与x轴交于点P（x，0），若直线AB与半圆弧有公共点，则x值的范围是（ ）| A． | -3≤x≤3$\sqrt{2}$ | B． | -3≤x≤3 | C． | -3$\sqrt{2}$≤x≤3 | D． | 0≤x≤3$\sqrt{2}$ |
6．方程x2-4x=0的解是（ ）
| A． | 0 | B． | 4 | C． | 0或-4 | D． | 0或4 |
平行四边形ABCD在平面直角坐标系中的位置如图所示，其中A（-6，0），B（4，0），C（5，3），反比例函数y=$\frac{k}{x}$的图象经过点C．
3．下列各式中，从左到右的变形是因式分解的是（ ）
| A． | a2c-a2b+1=a2（c-b）+1 | B． | a（x+y+1）=ax+ay+a | ||
| C． | （x+3y）（x-3y）=x2-9y2 | D． | 4x2-1=（2x+1）（2x-1） |