题目内容
13.规定:[x]表示不超过x的最大整数,例如:[3.69]=3,[-3.69]=-4,$[\sqrt{3}]=1$.计算:$[\sqrt{13}]-1$=2.分析 先依据被开方数越大对应的算术平方根越大估算出$\sqrt{13}$的大小,然后再求根据[x]的定义求得$\sqrt{13}$的值,最后依据减法法则求解即可.
解答 解:∵9<13<16,
∴3<$\sqrt{13}$<4.
∴[$\sqrt{13}$]=3.
∴$[\sqrt{13}]-1$=3-1=2.
故答案为:2.
点评 本题主要考查的是估算无理数的大小,估算出$\sqrt{13}$取值范围是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.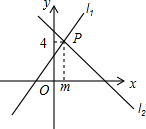 如图l1:y=x+3与l2:y=ax+b相交于点P(m,4),则关于x的不等式x+3≤ax+b的解为( )
如图l1:y=x+3与l2:y=ax+b相交于点P(m,4),则关于x的不等式x+3≤ax+b的解为( )
 如图l1:y=x+3与l2:y=ax+b相交于点P(m,4),则关于x的不等式x+3≤ax+b的解为( )
如图l1:y=x+3与l2:y=ax+b相交于点P(m,4),则关于x的不等式x+3≤ax+b的解为( )| A. | x≥4 | B. | x<m | C. | x≥m | D. | x≤1 |
8.已知P1(-1,y1),P2(2,y2)是一次函数y=-x+1图象上的两个点,则y1,y2的大小关系是( )
| A. | y1=y2 | B. | y1<y2 | C. | y1>y2 | D. | 不能确定 |
5.若一次函数y=(m-3)x+(m+1)(其中m为常数)的图形经过第一、二、四象限,则m的取值范围是( )
| A. | -1≤m≤3 | B. | m<3 | C. | -1<m<3 | D. | m>3 |
 如图,在?ABCD中,E,F分别在AD,BC上,且AE=CF,连结BE、DF.
如图,在?ABCD中,E,F分别在AD,BC上,且AE=CF,连结BE、DF.