题目内容
3.在平面直角坐标系中,边长为$\sqrt{2}$的正方形ABCD的对角线AC,BD相交于点P,顶点B,A在x,y轴正半轴上运动(x轴的正半轴,y轴的正半轴都不包含原点O)顶点C、D都在第一象限.(1)如图1,当∠ABO=45°时,求直线OP的解析式,并说明OP平分∠AOB;
(2)当∠ABO≠45°时(如图2):OP是否还平分∠AOB?点P是否仍在直线y=x上,若是,请选择图2进行证明;如若不是,请说明理由.
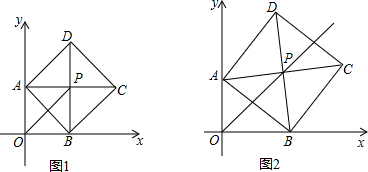
分析 (1)根据正方形的性质得出∠BPA=90°,PA=PB,再结合∠ABO=45°即可得出四边形OAPB是正方形.根据AB=$\sqrt{2}$结合勾股定理即可求出PA=PB=1,由此即可得出点P的坐标,利用待定系数法即可求出直线OP的解析式,再根据正方形的性质得出∠PAO=∠PBO=90°即PB⊥x轴,PA⊥y轴,依据角平分线的性质即可得出OP平分∠AOB;
(2)OP平分∠AOB,点P在直线y=x上.过点P作PE⊥x轴于点E,PF⊥y轴于点F,通过证明△EPB≌△FPA即可得出PE=PF,由此可得出OP平分∠AOB,设点P坐标为(m,n),则可得出m=n,由此即可得知点P在直线y=x上.
解答 (1)证明:∵∠BPA=90°,PA=PB,
∴∠PBA=45°,
∵∠ABO=45°,
∴∠PBO=90°,
∴四边形OAPB是正方形.
∵AB=$\sqrt{2}$,
由勾股定理得:PA=PB=1,
∴P点的坐标为(1,1).
设直线OP的解析式为y=kx,
把点P(1,1)代入y=kx得:1=k,
∴直线OP的解析式为y=x.
又∵四边形OAPB是正方形,
∴∠PAO=∠PBO=90°,
∴PB⊥x轴,PA⊥y轴,
又∵PA=PB,
∴OP平分∠AOB.
(2)解:OP平分∠AOB,点P在直线y=x上.
过点P作PE⊥x轴于点E,PF⊥y轴于点F,如图所示.
∵∠APE+∠EPB=90°,∠FPA+∠APE=90°,
∴∠EPB=∠FPA.
在△EPB和△FPA中,有$\left\{\begin{array}{l}{∠EPB=∠FPA}\\{∠PFA=∠PEB=90°}\\{PA=PB}\end{array}\right.$,
∴△EPB≌△FPA(AAS),
∴PE=PF.
∴OP平分∠AOB.
又∵PE=PF,
∴设点P(m,n),
则m=n,
∴点P在直线y=x上.
点评 本题考查了正方形的性质、待定系数法求函数解析式、角平分线的性质以及全等三角形的判定及性质,解题的关键是:(1)求出点P的坐标;(2)证出PE=PF.本题属于中档题,难度不大,解决该题型题目时,求出点的坐标,再利用待定系数法求出函数解析式是关键.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
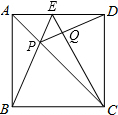 如图,已知正方形ABCD,E为AD的中点,连接BE和EC,BE交AC于点P,连接DP,交CE于Q.求证:
如图,已知正方形ABCD,E为AD的中点,连接BE和EC,BE交AC于点P,连接DP,交CE于Q.求证: 正方形ABCD中,点G为BC上任意一点,DE⊥AG于E,BF∥DE交AG于F.
正方形ABCD中,点G为BC上任意一点,DE⊥AG于E,BF∥DE交AG于F.