题目内容
1.已知$\frac{3a-b}{2b-a}$=7,$\frac{x+y}{2x-y}$=5,求$\frac{3ax-by}{ax+2by}$的值.分析 把已知的式子变形成a=$\frac{3}{2}$b和x=$\frac{2}{3}$y的形式,然后代入所求的代数式求解.
解答 解:∵$\frac{3a-b}{2b-a}$=7,
∴3a-b=14b-7a,
∴10a=15b,
∴2a=3b,
∴a=$\frac{3}{2}$b.
∵$\frac{x+y}{2x-y}$=5,
∴x+y=10x-5y,
则9x=6y,
∴x=$\frac{2}{3}$y.
∴原式=$\frac{3ax-by}{ax+2by}$=$\frac{3×\frac{3}{2}b•\frac{2}{3}y-by}{\frac{3}{2}b•\frac{2}{3}y+2by}$=$\frac{2by}{3by}$=$\frac{2}{3}$.
点评 本题考查了分式的化简求值,正确对已知的式子进行变形是解决本题的关键.

练习册系列答案
相关题目
11.计算:$\sqrt{17}÷\sqrt{85}•\sqrt{5}$=( )
| A. | 1 | B. | 3 | C. | 2 | D. | 4 |
 如图,直线a∥b,AC⊥BC,∠C=90°,∠2=65°,则∠1=25°.
如图,直线a∥b,AC⊥BC,∠C=90°,∠2=65°,则∠1=25°.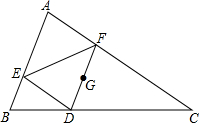 如图所示,在△ABC中,DF经过△ABC的重心G,且DF∥AB,DE∥AC,连接EF,如果BC=5,AC=$\sqrt{2}$AB,求证:△DEF∽△ABC.
如图所示,在△ABC中,DF经过△ABC的重心G,且DF∥AB,DE∥AC,连接EF,如果BC=5,AC=$\sqrt{2}$AB,求证:△DEF∽△ABC.