Question

6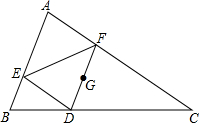．如图所示，在△ABC中，DF经过△ABC的重心G，且DF∥AB，DE∥AC，连接EF，如果BC=5，AC=$\sqrt{2}$AB，求证：△DEF∽△ABC．

Answer 1

分析 先判断四边形AEDF为平行四边形得到∠EDF=∠A，再根据三角形重心性质和平行线分线段成比例定理得到$\frac{DF}{AB}$=$\frac{CD}{BC}$=$\frac{2}{3}$，则CD=2BD，DF=$\frac{2}{3}$AB，接着由DE∥AC得到$\frac{DE}{AC}$=$\frac{BD}{BC}$=$\frac{1}{3}$，则DE=$\frac{1}{3}$AC，于是可计算出$\frac{DF}{DE}$=$\frac{2AB}{\sqrt{2}AB}$=$\sqrt{2}$，所以$\frac{DF}{AC}$=$\frac{DE}{AB}$，然后根据两组对应边的比相等且夹角对应相等的两个三角形相似即可得到结论．

解答 证明：∵DF∥AB，DE∥AC，
∴四边形AEDF为平行四边形，
∴∠EDF=∠A，
∵DF经过△ABC的重心G，且DF∥AB，
∴$\frac{DF}{AB}$=$\frac{CD}{BC}$=$\frac{2}{3}$，
∴CD=2BD，DF=$\frac{2}{3}$AB，
∵DE∥AC，
∴$\frac{DE}{AC}$=$\frac{BD}{BC}$=$\frac{1}{3}$，
∴DE=$\frac{1}{3}$AC，
∴$\frac{DF}{DE}$=$\frac{\frac{2}{3}AB}{\frac{1}{3}AC}$，
∵AC=$\sqrt{2}$AB，
∴$\frac{DF}{DE}$=$\frac{2AB}{\sqrt{2}AB}$=$\sqrt{2}$，
∴$\frac{DF}{DE}$=$\frac{AC}{AB}$，即$\frac{DF}{AC}$=$\frac{DE}{AB}$，
∵∠EDF=∠A，
∴△DEF∽△ABC．

点评 本题考查了相似三角形的判定：两组对应边的比相等且夹角对应相等的两个三角形相似．也考查了三角形重心的性质和平行线分线段成比例定理．