题目内容
9.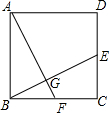 在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF,则下列结论中错误的是( )
在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF,则下列结论中错误的是( )| A. | ∠AFB+∠BEC=90° | B. | AF⊥BE | C. | ∠DAF=∠BEC | D. | BE=AF |
分析 正方形的四边相等,四个角都是直角,且BF=CE,很容易证明△ABF≌△BCE,从而判断结论的正误.
解答 解:∵AB=BC,∠ABF=∠BCE,BF=CE,
∴△ABF≌△BCE,
∴BE=AF.(故D正确).
∵△ABF≌△BCE,
∴∠AFB=∠BEC.
∵AD∥BC,
∴∠DAF=∠AFB=∠BEC,故C正确,
∵∠CBE+∠BEC=90°,
∴∠EBC+∠AFB=90°,
∴∠BGF=90°
∴AF⊥BE.(故B正确).
故选A.
点评 本题考查了正方形的性质和全等三角形的判定和性质,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
4.某市石化乙烯厂某车间生产甲、乙两种塑料的相关信息如下表,请你解答下列问题:
(1)设该车间每月生产甲、乙两种塑料各x吨,利润分别为y1元和y2元,分别求y1和y2与x的函数关系式(注:利润=总收入-总支出);
(2)已知该车间每月生产甲、乙两种塑料均不超过500吨,若某月要生产甲、乙两种塑料共700吨,求该月生产甲、乙塑料各多少吨,获得的总利润最大?最大利润是多少?
| 价目品种 | 出厂价 | 成本价 | 排污处理费 |
| 甲种塑料 | 2100(元/吨) | 800(元/吨) | 200(元/吨) |
| 乙种塑料 | 2400(元/吨) | 1100(元/吨) | 100(元/吨) 每月还需支付设备管理、 维护费20000元 |
(2)已知该车间每月生产甲、乙两种塑料均不超过500吨,若某月要生产甲、乙两种塑料共700吨,求该月生产甲、乙塑料各多少吨,获得的总利润最大?最大利润是多少?
1.下列图案中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为(3,$\frac{4}{3}$).
矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为(3,$\frac{4}{3}$).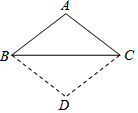 如图,已知△ABC,AB=AC,将△ABC沿边BC翻折,得到的△DBC与原△ABC拼成四边形ABDC.求证:四边形ABDC是菱形.
如图,已知△ABC,AB=AC,将△ABC沿边BC翻折,得到的△DBC与原△ABC拼成四边形ABDC.求证:四边形ABDC是菱形.