题目内容
14．
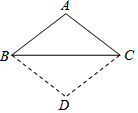如图，已知△ABC，AB=AC，将△ABC沿边BC翻折，得到的△DBC与原△ABC拼成四边形ABDC．求证：四边形ABDC是菱形．
分析 由翻转变换的性质得到BA=BD，CA=CD，根据题意得到AB=BD=DC=CA，根据菱形的判定定理证明．
解答 解：由翻转变换的性质可知，BA=BD，CA=CD，
∵AB=AC，
∴AB=BD=DC=CA，
∴四边形ABDC是菱形．
点评 本题考查的是翻转变换的性质、菱形的判定，掌握四条边相等的四边形是菱形是解题的关键．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
9．
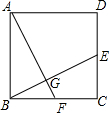在正方形ABCD中，点E、F分别在CD、BC上，且BF=CE，连接BE、AF，则下列结论中错误的是（ ）
在正方形ABCD中，点E、F分别在CD、BC上，且BF=CE，连接BE、AF，则下列结论中错误的是（ ）| A． | ∠AFB+∠BEC=90° | B． | AF⊥BE | C． | ∠DAF=∠BEC | D． | BE=AF |
如图，在平行四边形ABCD中，P是CD边上一点，且AP和BP分别平分∠DAB和∠CBA，若AD=5，AP=8，则△APB的周长是24．
3．
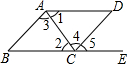如图，不能使AB∥CD的是（ ）
如图，不能使AB∥CD的是（ ）| A． | ∠3=∠4 | B． | ∠1=∠2 | C． | ∠B=∠5 | D． | ∠B+∠BCD=180° |