题目内容
20. 矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为(3,$\frac{4}{3}$).
矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为(3,$\frac{4}{3}$).
分析 如图,作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小,先求出直线CH解析式,再求出直线CH与AB的交点即可解决问题.
解答 解: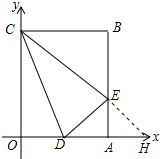 如图,作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小.
如图,作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小.
∵D($\frac{3}{2}$,0),A(3,0),
∴H($\frac{9}{2}$,0),
∴直线CH解析式为y=-$\frac{8}{9}$x+4,
∴x=3时,y=$\frac{4}{3}$,
∴点E坐标(3,$\frac{4}{3}$),
故答案为:(3,$\frac{4}{3}$).
点评 本题考查矩形的性质、坐标与图形的性质、轴对称-最短问题、一次函数等知识,解题的关键是利用轴对称找到点E位置,学会利用一次函数解决交点问题,属于中考常考题型.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
8.下列命题中,是真命题的是( )
| A. | 相等的角是对顶角 | B. | 互补的角是邻补角 | ||
| C. | 同旁内角是互补的角 | D. | 邻补角是互补的角 |
12.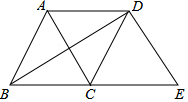 如图,将△ABC沿BC方向平移得到△DCE,连接BD,AD,下列条件不能判定四边形ABCD是菱形的是( )
如图,将△ABC沿BC方向平移得到△DCE,连接BD,AD,下列条件不能判定四边形ABCD是菱形的是( )
 如图,将△ABC沿BC方向平移得到△DCE,连接BD,AD,下列条件不能判定四边形ABCD是菱形的是( )
如图,将△ABC沿BC方向平移得到△DCE,连接BD,AD,下列条件不能判定四边形ABCD是菱形的是( )| A. | ∠ABC=∠ACB | B. | AB=AD | C. | ∠BAC=∠DAC | D. | AC⊥BD |
9.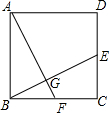 在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF,则下列结论中错误的是( )
在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF,则下列结论中错误的是( )
 在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF,则下列结论中错误的是( )
在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF,则下列结论中错误的是( )| A. | ∠AFB+∠BEC=90° | B. | AF⊥BE | C. | ∠DAF=∠BEC | D. | BE=AF |
10. 如图,已知∠1=∠B,则下列结论错误的是( )
如图,已知∠1=∠B,则下列结论错误的是( )
 如图,已知∠1=∠B,则下列结论错误的是( )
如图,已知∠1=∠B,则下列结论错误的是( )| A. | AD∥BC | B. | ∠2+∠B=180° | C. | ∠2=∠C | D. | ∠C+∠D=180° |