题目内容
17.解方程组或不等式组(1)$\left\{\begin{array}{l}{x-y=2}\\{x-2y=-3}\end{array}\right.$
(2)解不等式$\frac{2x-1}{3}$-$\frac{5x+1}{2}$≥1,把它的解集在数轴上表示出来.
分析 (1)加减消元法求解可得;
(2)根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得.
解答 解:(1)$\left\{\begin{array}{l}{x-y=2}&{①}\\{x-2y=-3}&{②}\end{array}\right.$,
①-②,得:y=5,
将y=5代入①,得:x-5=2,
解得:x=7,
则$\left\{\begin{array}{l}{x=7}\\{y=5}\end{array}\right.$;
(2)去分母,得:2(2x-1)-3(5x+1)≥6,
去括号,得:4x-2-15x-3≥6,
移项、合并,得:-11x≥11,
系数化为1,得:x≤-1,
将解集表示在数轴上如下:
点评 本题主要考查解二元一次方程组和一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.

练习册系列答案
相关题目
12.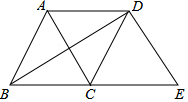 如图,将△ABC沿BC方向平移得到△DCE,连接BD,AD,下列条件不能判定四边形ABCD是菱形的是( )
如图,将△ABC沿BC方向平移得到△DCE,连接BD,AD,下列条件不能判定四边形ABCD是菱形的是( )
 如图,将△ABC沿BC方向平移得到△DCE,连接BD,AD,下列条件不能判定四边形ABCD是菱形的是( )
如图,将△ABC沿BC方向平移得到△DCE,连接BD,AD,下列条件不能判定四边形ABCD是菱形的是( )| A. | ∠ABC=∠ACB | B. | AB=AD | C. | ∠BAC=∠DAC | D. | AC⊥BD |
9.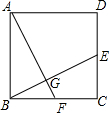 在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF,则下列结论中错误的是( )
在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF,则下列结论中错误的是( )
 在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF,则下列结论中错误的是( )
在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF,则下列结论中错误的是( )| A. | ∠AFB+∠BEC=90° | B. | AF⊥BE | C. | ∠DAF=∠BEC | D. | BE=AF |
 如图,在平行四边形ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是24.
如图,在平行四边形ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是24.