题目内容
如图，AB是⊙O的直径，AB垂直于弦CD，∠BOC=70°，则∠ABD=考点：垂径定理
专题：
分析：根据圆周角定理求出∠BDC，求出∠BMD，根据三角形内角和定理求出即可．
解答：解：∵∠BOC=70°，
∴∠BDC=
∠BOC=35°，
∵DC⊥AB，
∴∠DMB=90°，
∴∠ABD=180°-∠BDC-90°=55°，
故答案为：55．
∴∠BDC=
| 1 |
| 2 |
∵DC⊥AB，
∴∠DMB=90°，
∴∠ABD=180°-∠BDC-90°=55°，
故答案为：55．
点评：本题考查了三角形内角和定理和圆周角定理的应用，根据圆周角定理求出∠BDC的度数是解此题的关键．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
相关题目
已知：如图所示的一张矩形纸片ABCD（AD＞AB），将纸片折叠一次，使点A与点C重合，再展开，折痕EF交AD边于点E，交BC边于点F，分别连结AF和CE．
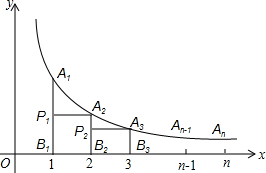如图，在反比例函数y=
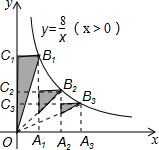如图，A1、A2、A3…An在x轴上，且OA1=A1A2=A2A3=…=An-1An，分别过点A1、A2、A3…An作y轴的平行线，与反比例函数y=