题目内容
 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.(1)求证:四边形AFCE是菱形;
(2)若AB=4,BC=8,求△ABF的面积;
(3)在线段AC上是否存在一点P,使得AE2=AO•AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.
考点:矩形的性质,菱形的判定,翻折变换(折叠问题),相似三角形的判定与性质
专题:
分析:(1)根据矩形的性质AD∥BC,根据两直线平行,内错角相等可得∠EAO=∠FCO,再利用“角边角”证明△AEO和△CFO全等,根据全等三角形对应边相等可得AE=CF,然后根据一组对边平行且相等的四边形是平行四边形,再根据翻折的性质可得AE=CE,然根据邻边相等的平行四边形是菱形证明即可;
(2)设BF=x,再表示出AF,然后利用勾股定理列式求出x,再利用三角形的面积列式计算即可得解;
(3)过点E作AD的垂线,交AC于点P,求出△AOE和△AEP相似,再根据相似三角形对应边成比例解答.
(2)设BF=x,再表示出AF,然后利用勾股定理列式求出x,再利用三角形的面积列式计算即可得解;
(3)过点E作AD的垂线,交AC于点P,求出△AOE和△AEP相似,再根据相似三角形对应边成比例解答.
解答:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EAO=∠FCO,
由折叠的性质,OA=OC,∠AOE=∠COF,
在△AEO和△CFO中,
,
∴△AEO≌△CFO(ASA),
∴AE=CF,
∵AE∥FC,
∴四边形AFCE是平行四边形,
∵EF为对称轴,
∴AE=CE,
∴四边形AFCE菱形;
(2)解:设BF=x,∵四边形AECF是菱形,
∴AF=FC=8-x,
∵ABCD是矩形,
∴∠B是直角,
∴(8-x)2=42+x2,
解得x=3,
∴S△ABF=
×3×4=6;
(3)存在.过点E作AD的垂线,交AC于点P,点P就是符合条件的点.
证明:∵∠AEP=∠AOE=90°,∠EAO=∠EAP
∴△AOE∽△AEP,
∴
=
,
∴AE2=AO•AP.
∴AD∥BC,
∴∠EAO=∠FCO,
由折叠的性质,OA=OC,∠AOE=∠COF,
在△AEO和△CFO中,
|
∴△AEO≌△CFO(ASA),
∴AE=CF,
∵AE∥FC,
∴四边形AFCE是平行四边形,
∵EF为对称轴,
∴AE=CE,
∴四边形AFCE菱形;
(2)解:设BF=x,∵四边形AECF是菱形,
∴AF=FC=8-x,
∵ABCD是矩形,
∴∠B是直角,
∴(8-x)2=42+x2,
解得x=3,

∴S△ABF=
| 1 |
| 2 |
(3)存在.过点E作AD的垂线,交AC于点P,点P就是符合条件的点.
证明:∵∠AEP=∠AOE=90°,∠EAO=∠EAP
∴△AOE∽△AEP,
∴
| AE |
| AO |
| AP |
| AE |
∴AE2=AO•AP.
点评:本题考查了矩形的性质,菱形的判定与性质,翻折变换的性质,相似三角形的判定与性质,勾股定理的应用,熟记各性质以及菱形的判定方法是解题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
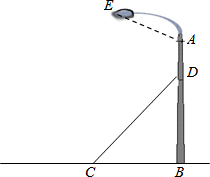 如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成37°夹角,且CB=4米.
如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成37°夹角,且CB=4米.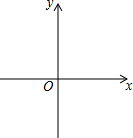 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.在新图形中你发现了什么?请写出一条;在若点P的坐标为(2a,b+1),则a与b的数量关系为
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.在新图形中你发现了什么?请写出一条;在若点P的坐标为(2a,b+1),则a与b的数量关系为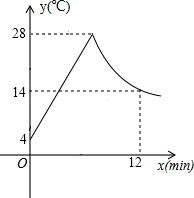 如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14℃.
如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14℃.
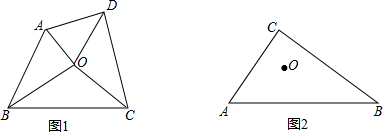
 如图,AB是⊙O的直径,AB垂直于弦CD,∠BOC=70°,则∠ABD=
如图,AB是⊙O的直径,AB垂直于弦CD,∠BOC=70°,则∠ABD=