Question

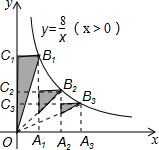如图，A₁、A₂、A₃…A_n在x轴上，且OA₁=A₁A₂=A₂A₃=…=A_n-1A_n，分别过点A₁、A₂、A₃…A_n作y轴的平行线，与反比例函数y=

8

x

（x＞0）的图象分别交于点B₁、B₂、B₃…B_n，分别过点B₁、B₂、B₃…B_n作x轴的平行线，分别与y轴交于点C₁、C₂、C₃…C_n，连接OB₁、OB₂、OB₃…OB_n得到n个阴影三角形，那么图中第n个阴影三角形的面积是

 

．

Answer 1

考点：反比例函数系数k的几何意义

专题：规律型

分析：根据反比例函数的比例系数k的几何意义得到第1个阴影三角形的面积=4，由于第2个阴影三角形与三角形OB₂C₂相似，根据相似得性质得则第2个阴影三角形的面积=

1

4

S_△OB2C2=

4

4

，同理可得第3个阴影三角形的面积=

1

9

S_△OB3C3=（

1

3

）²×

1

2

×8=

4

9

，于是得到第n个阴影三角形的面积=

1

4

S_△OBnCn=（

1

n

）²×

1

2

×8=

4

n2

．

解答：解：第1个阴影三角形的面积=

1

2

×8=4，
第2个阴影三角形的面积=

1

4

S_△OB2C2=（

1

2

）²×

1

2

×8=

4

4

，
第3个阴影三角形的面积=

1

9

S_△OB3C3=（

1

3

）²×

1

2

×8=

4

9

，
所以第n个阴影三角形的面积=

1

4

S_△OBnCn=（

1

n

）²×

1

2

×8=

4

n2

．
故答案为

4

n2

．

点评：本题考查了反比例函数的比例系数k的几何意义：在反比例函数y=

k

x

图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．也考查了相似三角形面积的比等于相似比的平方．