题目内容
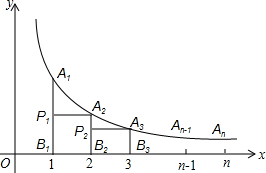 如图,在反比例函数y=
如图,在反比例函数y=| 2 |
| x |
考点:反比例函数系数k的几何意义,反比例函数图象上点的坐标特征
专题:规律型
分析:求出x=2所对应的函数值即可确定A2的坐标;根据反比例函数图象上点的坐标特征和三角形面积公式得到S1=
×1×(2-1),S2=
×1×(1-
),S3=
×1×(
-
),…,Sn=
×1×(
-
),然后把它们相加后合并即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 4 |
| 1 |
| 2 |
| 2 |
| n |
| 2 |
| n+1 |
解答:解:把x=2代入y=
得y=1,
∴点A2的坐标为(2,1);
∵S1=
×1×(2-1),S2=
×1×(1-
),S3=
×1×(
-
),…,Sn=
×1×(
-
),
∴S1+S2+…+Sn=
(2-1+1-
+
-
+…+
-
)=
(2-
)=
.
故答案为(2,1);
.
| 2 |
| x |
∴点A2的坐标为(2,1);
∵S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 4 |
| 1 |
| 2 |
| 2 |
| n |
| 2 |
| n+1 |
∴S1+S2+…+Sn=
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 4 |
| 2 |
| n |
| 2 |
| n+1 |
| 1 |
| 2 |
| 2 |
| n+1 |
| n |
| n+1 |
故答案为(2,1);
| n |
| n+1 |
点评:本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=
图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
| k |
| x |

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
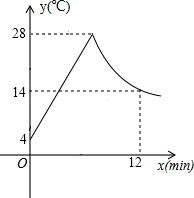 如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14℃.
如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14℃.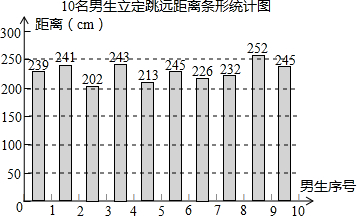
 如图,AB是⊙O的直径,AB垂直于弦CD,∠BOC=70°,则∠ABD=
如图,AB是⊙O的直径,AB垂直于弦CD,∠BOC=70°,则∠ABD= 如图,梯形ABCD中,AD∥BC,AD=3,BC=7,E、F分别是AB、CD的中点,G在BC上,EG∥AF,则CG的长等于
如图,梯形ABCD中,AD∥BC,AD=3,BC=7,E、F分别是AB、CD的中点,G在BC上,EG∥AF,则CG的长等于